Углы вписанного в окружность треугольника - вписанные. Вписанный угол измеряется половиной дуги, на которую он опирается.
Полная окружность содержит 360°.
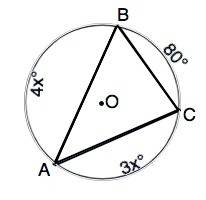
◡ВАС=360°-80°=280°
АВ:АС=4:3
Примем коэффициент этого отношения равным х.
Дуга ВАС состоит из ◡АВ+◡АС и равна .
4х+3х=7х
х=280°:7=40° – содержит каждая часть ◡ВАС
◡АС=3•40°=120°
◡АВ=4•40°=160°
Угол А опирается на дугу ВС и равен ее половине:
∠А=80°:2=40°
Угол В опирается на дугу АС и равен ее половине:
∠В=120:2=60°
Угол С опирается на дугу АВ и равен ее половине:
∠С=160°:2=80°
Треугольник ABC - равнобедренный с вершиной С, угол A при основании.
Проводим высоту СН. В прямоугольном треугольнике AСH имеем:
tg(A) = СH/AH
Точка H - середина AB (по свойству равнобедренного треугольника),
тогда AH = AB/2 = 4
В прямоугольном треугольнике AСH гипотенуза AС = 5, тогда по теореме Пифагора имеем СH =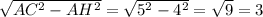
Следовательно tg(A) = СH/AH = 3/4