Сумма острых углов прямоугольного треугольника 90°. Поэтому сумма их половин равна 45°, и величина углов, образуемых их биссектрисами, всегда будет 45° и 135°.
По условию угол, образуемый биссектрисами, равен 70°, следовательно, одна из биссектрис проведена из прямого угла.
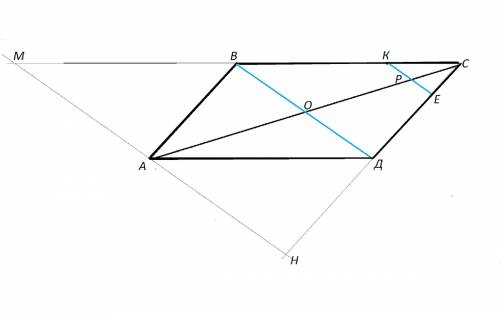
Обозначим вершины треугольника А, В, С. Биссектрисы СМ и АК. Точка пересечения биссектрис О.
∠МОА=70°
∠ОСА=45°.
∠МОА - внешний для ∆ СОА и равен сумме внутренних не смежных с ним углов. ⇒
∠ОАС=70°- 45°=25°⇒
∠ВАС=2•25°=50°
∠АВС=90°-50°=40°.
ответ: 50° и 40°.
Проведём высоту ВД на АС. В равнобедренном треугольнике она также будет медианой и биссектрисой. Значит точка лежит на ВД. По теореме Пифогора ВД= корень из(АВ квадрат-АД квадрат)=корень из(100-64)=6. Точка пересечения медиан делит их в отношении 2/1 считая от вершины. То есть ВО/ОД=2/1. Или ВО=2ОД. ВО+ОД=6. Отсюда ВО=4. ОД=2. Расстояние АО=корень из (АД квадрат+ОД квадрат)= корень из(64+4)=2 корня из 17.