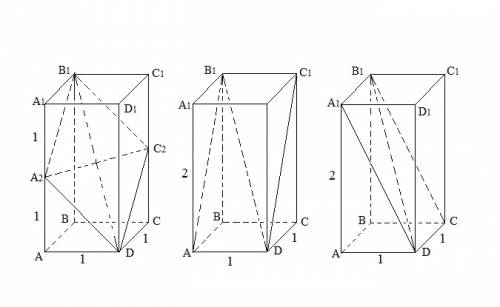
A2C2 = A2D = √(1² + 1²) =√2;
B1D = √(1² + 1² + 2²) = √6;
S = 1/2D*d;
S A2B1C2D = 1/2√6 * √2 = √12/2 = √3.
Проверим, действительно ли площадь ромба A2B1C2D меньше площади прямоугольника AB1C1D.
AD = 1;
AB1 = √(1² + 2²) = √5;
S AB1C1D = 1 * √5 = √5.
ответ: √3.
ответ: 100°
Объяснение:
Сумма острых углов прямоугольного треугольника 90°.
⇒ Угол МКN=90°-35°=55°
∠SKN=55°-10°=45°. ,∠KSN=90°-45°=45° ⇒ ∆ KNS - равнобедренный. КN=SN.
С другой стороны, в ∆ PNK угол РNK=∠SNK-∠SNP=90°-20°=70°. Отсюда ∠КРN=180°-70°-55°=55°, ⇒ ∆ PNK –равнобедренный. PN=NK. Но NK=NS ⇒ NS=NP и ∆ SNP равнобедренный. ∠NSP=∠NPS =(180°-20°):2=80°
Смежный углу NSP искомый угол PSM=180°-80°=100°.