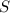 данного сечения =
данного сечения = 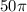 ед.кв.
ед.кв.
Объяснение:
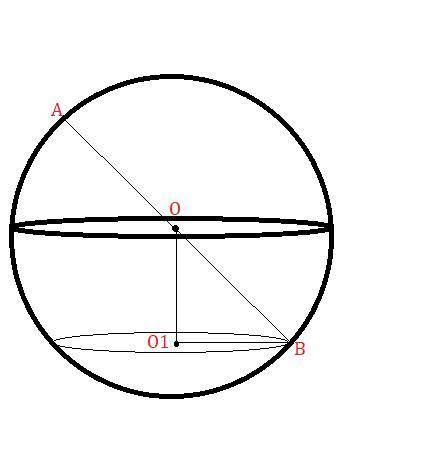
Пусть будет дан шар с центром в точке 
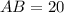 ед.
ед.
Через точку 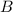 проведём плоскость под углов
проведём плоскость под углов 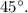
Пусть будет плоскость с центром в точке 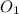 .
.
Тогда 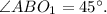
========================================================
Так как 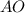 и
и 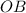 - радиусы данного шара
- радиусы данного шара 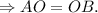
Т.е. 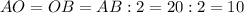 ед.
ед.
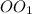
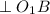 , так как
, так как 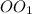 - серединный перпендикуляр.
- серединный перпендикуляр.
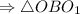 - прямоугольный.
- прямоугольный.
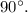
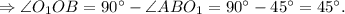
Так как 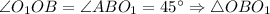 - равнобедренный.
- равнобедренный.
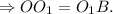
Пусть  -
- 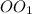 и
и 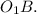
По теореме Пифагора:
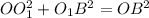
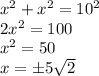
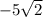 - отрицательное число, поэтому не подходит.
- отрицательное число, поэтому не подходит.
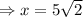
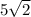 ед. -
ед. - 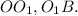
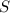 данного сечения =
данного сечения = 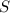 круга =
круга = 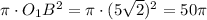 ед.кв.
ед.кв.

ВС=АД= 9 см
Диагональ АС= а
Диагональ ВД=b
Так как сумма квадратов диагоналей = сумме квадратов его сторон, то
a^2 + b^2= АВ^2 + СД^2 + ВС^2 +АД^2=260
a+b=22 (из условия)
а=22-b
(22-b)^2 + b^2 = 260
раскрываем скобки
484-44*b + b^2 + b^2 = 260
2*b^2 - 44*b + 224 = 0 делим на 2
b^2 - 22*b + 112 =0
уровнение имеет два действительных корня
b_{1}b1 = 8
b_{2}b2 = 14
если диагональ ВД= b_{1}b1 = 8 см, то диагональ АС=22-8=14 см и наоборот
если диагональ ВД= b_{2}b2 = 14 см, то диагональ АС = 22-14 = 8 см