N1. ответ во вложении.
N2.Дано:
MN=7
NK=12
KM=11
Найти:
NF=?
ME=?
KP=?
1)Если из точки к окружности проведены две касательные, то длины отрезков от этой точки до точек касания равны. Отсюда:
NE=NF=x
ME=MP=y
KP=KF=z
2)Составляем систему уравнений:
1.x+y=7 получаем: x=7-y
2.x+z=12 подставляем:
7-y+z=12
z=12-7+y
z=5+y
3.y+z=11 подставляем:
y+5+y=11
2y=6
y=3
ME=3
4.x=7-y=7-3=4
NF=4
5.z=5+y=5+3=8
KP=8
ответ: ME=3, NF=4, KP=8
N3. 1)360°=3x+7x+8x
360=18x
x=20°
2)ABдуга=3х=3*20=60
BCдуга=7х=7*20=140
ACдуга=8х=8*20=160
3) Вписанный угол в два раза меньше дуги, на которую он опирается.
Поэтому <А=140/2=70
<B=160/2=80
<C=60/2=30
ответ: <А=70
<B=80
<C=30
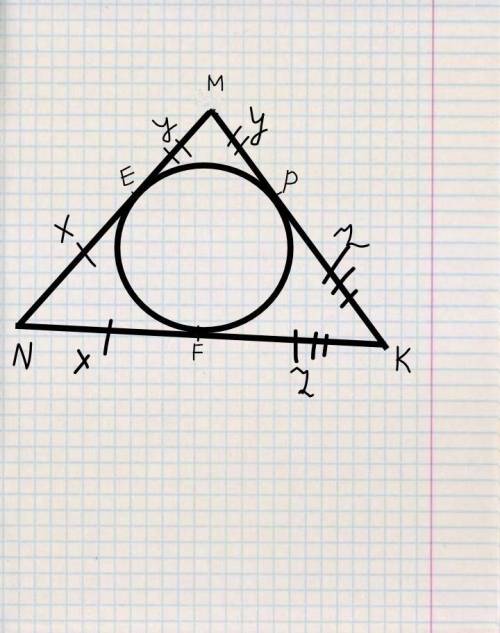
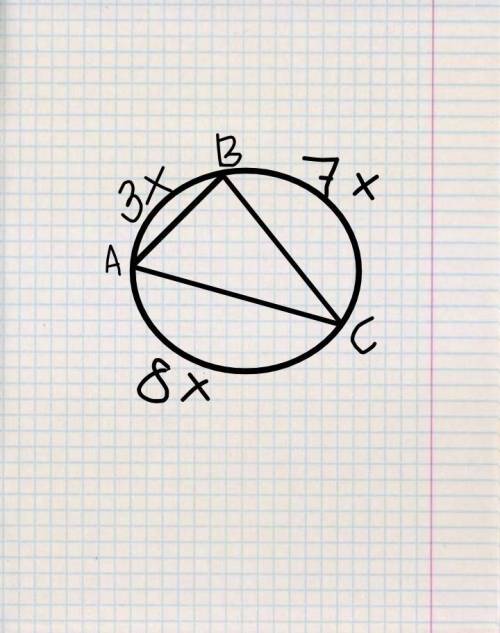
Объяснение: ЗАДАНИЕ 4
r=a×sinA/2, где а сторона ромба
r=12×sin30°/2=12×½/2=6/2=3см
r=3см. Длина окружности вычисляется по формуле: 2πr: длина окружности=2×3,14×3=18,84см
ответ: длина окружности=18,84см
ЗАДАНИЕ 5
Обозначим эти пропорции как 7х и 5х. Зная что периметр =44, составим уравнение:
7х+5х+8=44
12х+8=44
12х=44-8
12х=36
х=36÷12
х=3
Если х=3, то сторона2=7×3=21см
Сторона3=5×3=15см
Теперь найдём площадь треугольника через полупериметр:
р=44÷2=22см по формуле:
S=√((p(p-a)(p-b)(p-c)), где р- полупериметр, а, b, c стороны треугольника:
S=√((22(22-8)(22-21)(22-15))=
=√(22×14×1×7)=√2156=√(4×7×7×11)=
=2×7√11=14√11см²
ответ: S=14√11см²
ЗАДАНИЕ 6
Так как длина окружности =2πr, вычислим радиус, используя эту формулу:
2πR=12
R=12÷2π
R=6÷3,14
R=6/3,14см
R≈1,91см
Радиус в прямоугольнике равен половине его диагонали и Если рассмотреть треугольник, с углом между диагоналями 60°, то его стороны образуемые диагоналями будут равны поскольку в прямоугольнике они делятся пополам и равны радиусу. Если две стороны в треугольнике с углом 60° равны, то этот треугольник равносторонний. Поэтому одна из сторон =радиусу=1,91см. Диагональ прямоугольника делит его на 2 равных прямоугольных треугольника в котором диагональ является гипотенузой, и сейчас мы можем найти вторую сторону прямоугольника по теореме Пифагора:
Диагональ=1,91×2=3,82см
Сторона2=√(3,82²-1,91²)=
=√(14,5924-3,6481)=√10,9443≈3,31см
ответ: сторона1≈1,91см, сторона2≈3,31см
Отношение сторон треугольника запишем в виде: 6*Х+8*Х+10*Х=120
24*Х=120
Х=5, т.о. Стороны равны 30, 40, 50.
каждая сторона треугольника образованного серединами сторон является средней линией треугольника АВС, т.к средняя линия треугольника соединяющая середины его сторон параллельна третьей стороне и равна её половине(по определению средней линии), то периметр треугольника НМN равен: Р=15+20+25=60.