7) В(2; 1; -3) и С(-2; 1; -3)
8) А (-1; 0; 2)
9) длина медианы = 7
Объяснение:
7)
координаты точек прямой, параллельной оси абсцис будут иметь одинаковые координаты, кроме координаты х
это точки В(2; 1; -3) и С(-2; 1; -3)
8)
Вычислим вектор ВС (разности соотв координат точек) и посторим такой же вектор СА - получим точку А
С(0; 2; -3) В(1; 4; -8) вектор ВС = С()-В() = (-1; -2; 5)
Точка А() = С() + вектор ВС = (0-1; 2-2; -3+5) = (-1; 0; 2)
ответ: А (-1; 0; 2)
9)
Медиана делит отрезок пополам. Координаты соответствующей точки - среднее армфм соотв координат концов отрезка.
Зная координаты концов отрезка его длина вычисляется по формуле.
А(3; 0; 5), В(4; 3; -5), С(-4; 1; 3)
Пусть серединой ВС будет точка О()
О() = ((4+(-4))/2; (3+1)/2; (-5+3)/2;) = (0; 2; -1)
O(0; 2; -1)
Отрезок АО будет медианой ΔАВС из вершины А
Длина отрезка АО равна:
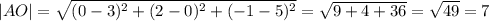
ответ: 7
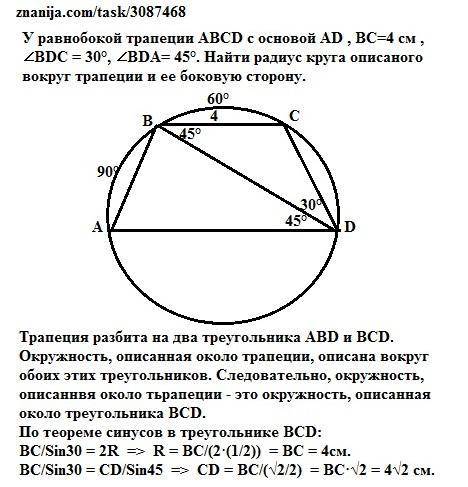
R = 4см. АВ = CD = 4√2 см.
Объяснение:
Трапеция разбита на два треугольника ABD и BСD. Окружность, описанная около трапеции, описана вокруг обоих этих треугольников. Следовательно, окружность, описаннвя около тьрапеции - это окружность, описанная около треугольника ВСD.
∠CBD = ∠BDA = 45° как внутренние еакрест лежащие углы при параллельных AD и ВС и секущей BD.
По теореме синусов в треугольнике ВСD:
ВС/Sin30 = 2R => R = BC/(2·(1/2)) = ВC = 4см.
ВС/Sin30 = СD/Sin45 => CD = BC/(√2/2) = ВC·√2 = 4√2 см.
X+16+x=180
2x+16=180
2x=164
X=82
82+16=98
У параллелограма противолежащие углы равны.
ответ:98,82