|AC| = 10 см.
Объяснение:
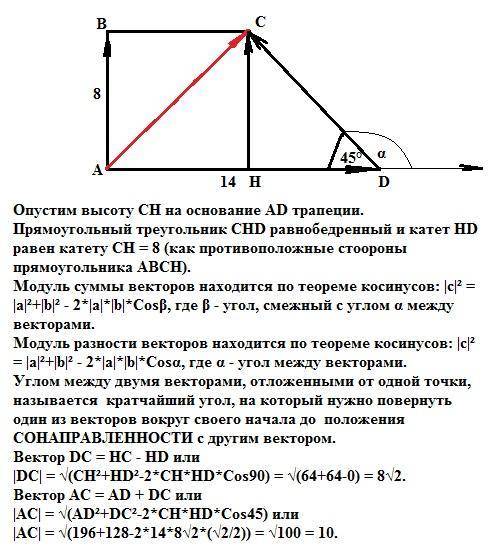
Опустим высоту СН на основание AD трапеции.
Прямоугольный треугольник СНD равнобедренный и катет HD равен катету СН = 8 (как противоположные стоороны прямоугольника АВСН).
Модуль суммы векторов находится по теореме косинусов: |c|² = |a|²+|b|² - 2*|a|*|b|*Cosβ, где β - угол, смежный с углом α между векторами.
Модуль разности векторов находится по теореме косинусов: |c|² = |a|²+|b|² - 2*|a|*|b|*Cosα, где α - угол между векторами.
Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения СОНАПРАВЛЕННОСТИ с другим вектором. Итак,
Вектор DC = НС - HD или
|DC| = √(CH²+HD²-2*CH*HD*Cos90) = √(64+64-0) = 8√2.
Вектор АС = AD + DC или
|AC| = √(AD²+DC²-2*CH*HD*Cos45) или
|AC| = √(196+128-2*14*8√2*(√2/2)) = √100 = 10.
ответ: Длина вектора (модуль) АС = 10 см.
Уравнение биссектрисы первой координатной четверти
y = x
Пусть координата центра окружности О(x; x)
Квадрат расстояния от центра окружности до точки (5; 3)
l² = (x - 5)² + (x - 3)² = 10
x² - 10x + 25 + x² - 6x + 9 = 10
2x² - 16x + 24 = 0
x² - 8x + 12 = 0
Дискриминант
D = 64 - 4*12 = 16
Корни
x₁ = (8 - 4)/2 = 2
x₂ = (8 + 4)/2 = 6
Оба решения годятся.
Первое
О₁(2; 2)
(x - 2)² + (y - 2)² = 10
Второе
О₂(2; 2)
(x - 6)² + (y - 6)² = 10