Объяснение: 1дм-10см
ответ: Ѕ=h₁•h₂/sinα
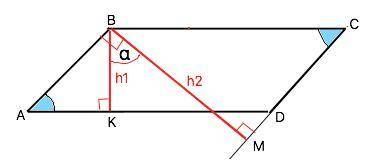
Объяснение: На приложенном рисунке - АВСD- параллелограмм; ВК и ВМ - его высоты.
Из условия ВК=h₁; BM=h₂, угол КВМ=α.
По одной из формул площадь параллелограмма равна произведению соседних сторон на синус угла между ними.
S(ABCD)=AB•АD•sin(BAD).
Высоты параллелограмма перпендикулярны двум его противоположным сторонам.⇒
Треугольники АВК и ВСМ - прямоугольные.
Сумма острых углов прямоугольного треугольника равна 90°, поэтому в ⊿ АВК ∠АВК=90°-∠ ВАК. Но ∠АВМ =90°, ⇒
∠АВК =90°-угол α ⇒
90°-угол ВАК=90°-угол α. ⇒
∠ ВАК =α.
Противоположные углы параллелограмма равны.
Из ⊿ АВК h₁=AB•sinα ⇒ AB=h₁:sinα
Из⊿ СВМ h₂=BC•sinα ⇒ BC=h₂:sinα
Ѕ(ABCD)=AB•BC•sinα=(h₁:sinα)•(h₂:sinα)•sinα=h₁•h₂/sinα.
Объяснение:
Средние линии треугольника - отрезки, соединяющие середины его сторон. Треугольник, образованный средними линиями, подобен исходному, поэтому отношение сторон обоих треугольников одинаково. Если стороны исходного треугольника а, b, c, то средние линии равны 0,5а, 0,5b и 0,5 с.
Соответственно, 0,5а:0,5b:0,5 с= а:b:с.
НО!
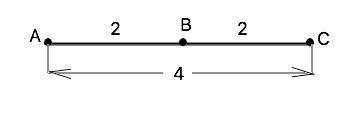
Треугольник с отношением сторон 2:2:4 не существует. По теореме . о неравенстве треугольника любая его сторона меньше суммы двух других. По данному отношению 4=2+2 все вершины лежат на одной прямой. (Треугольник, у которого все три вершины лежат на одной прямой, называется вырожденным - см. рисунок во вложении. ).
* * *
В сети встречается (и не раз!) задача, к которой дается решение без указания на неравенство треугольника, с таким условием:
Средние линии треугольника относятся как 2:2:4, а периметр треугольника равен 45 см. Найдите стороны треугольника. Ход решения верный, в ответе: а = b = 11,25; c = 22,5 см.
Получается, что с=а+b. Возможно, условие специально составлено так, чтобы решающий нашел в нем указанную выше ошибку.
16см
Объяснение:
1дм=10см
10см+ 2см+4см=16см