Объяснение:
Если отношения сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой, то треугольники подобны.
Расположим стороны в порядке возрастания и найдём их отношения:
1 треугольник: АВ = 20 см, ВС = 25 см, АС = 35 см
2треугольник: МР = 8 см, КР = 10 см, МК = 14 см
20/8=2,5
25/10=2,5
35/14=2,5
Следовательно треугольник АВС подобен треугольнику МРК с коэффициентом подобия k= 2,5 (3 признак подобия)
Коэффициентом подобия называют число k, равное отношению сходственных сторон подобных треугольников.Соответственные стороны подобных треугольников пропорциональны:
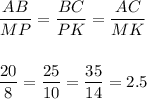
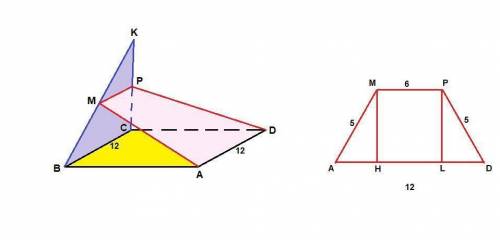
1) MPDA - равнобедренная трапеция
2) 36 см²
Объяснение:
1) МР - средняя линия треугольника ВСК, поэтому
МР║ВС и МР = 1/2 ВС = 6 см
МР║ВС, ВС║AD, ⇒ МР║AD.
Значит, MPDA трапеция. А так как МА = PD = 5 см, то
MPDA - равнобедренная трапеция.
2) Проведем высоты трапеции МН и PL. MPLH - прямоугольник, так как у него все углы прямые, тогда
HL = MP = 6 см.
ΔАМН = ΔDPL по гипотенузе и катету (∠АНМ = ∠DLP = 90°, так как проведены высоты, АМ = DP по условию и МН = PL как высоты), значит
АН = DL = (AD - HL)/2 = (12 - 6)/2 = 3 см
ΔАМН: прямоугольный, египетский, значит МН = 4 см.
Smpda = (MP + AD)/2 · MH = (6 + 12)/2 · 4 = 36 см²
1) 27-15=12см
Либо
2) 27+15=42см