1. На данной прямой а отметим произвольную точку А.
2. Проведем окружность произвольного радиуса с центром в точке А. Точки пересечения окружности с прямой а обозначим В и С.
3. Проведем две окружности одинакового произвольного радиуса (большего половины отрезка ВС), с центрами в точках В и С.
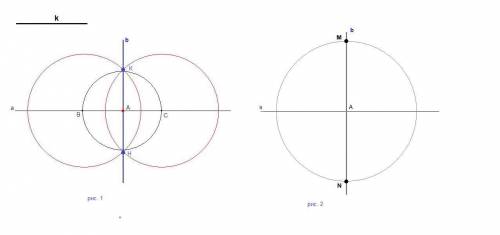
4. Через точки пересечения этих окружностей (К и Н) проведем прямую b.
Прямая b - искомый перпендикуляр к прямой а. (см. рис. 1)
5. Проведем окружность с центром в точке А с радиусом, равным данному отрезку k. Точки пересечения этой окружности с прямой b обозначим M и N. (см. рис. 2)
Точки М и N - точки, удаленные от точки пересечения прямых на расстояние, равное длине данного отрезка.
Все построение надо выполнять, конечно, на одном чертеже. Для наглядности построение последнего пункта выполнено отдельно.
Периметр это сумма всех сторон у параллелограмма параллельные стороны равны, значит какие-то две стороны равны 2(1 номер), 3( 2 номер) 1) х+2+2+х=32 2х=32-4 2х=28 х=14 две стороны равны 2, другие две стороны равны 14 2)х+3+3+х=32 2х=32-6 2х=26 х=13 две стороны. равны 2 см, две другие стороны равны 13 см. 5.0