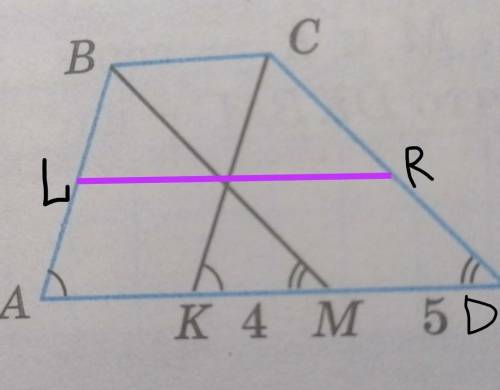
Пусть LR – средняя линия трапеции ABCD
Угол CDA=угол BMA по условию, тогда прямые CD u BM – паралельны, а углы CDA и BMA – соответственные при параллельных прямых CD u BM и секущей AD.
ВС//AD (так как основания трапеции параллельны) => ВС//MD
Исходя из найденного: BCDM – параллелограмм, так как его стороны попарно параллельны.
Следовательно ВС=MD=5 так как противоположные стороны параллелограмма равны.
Угол BAD=угол CKD по условию, тогда прямые BA u CK – паралельны, а углы BAD и CKD – соответственные при параллельных прямых ВА u СК и секущей AD.
ВС//AD (так как основания трапеции параллельны) => ВС//AK
Исходя из найденного: BCKA – параллелограмм, так как его стороны попарно параллельны.
Следовательно AK=ВС=5 так как противоположные стороны параллелограмма равны.
Средняя линия трапеции равна полусумме оснований.
Тоесть LR=(BC+AD)÷2
BC=5 (найдено ранее);
АD=AK+KM+MD=5+4+5=14
Тогда LR=(5+14)÷2=9,5
ответ: 9,5
Пусть угол А=90°
Рассмотрим параллелограмм ABCD.
Углы A и B - внутренние односторонние при BC||AD и секущей AB. Сумма внутренних односторонних углов равна 180°. Следовательно угол В = 180°- угол А = 180°-90°=90°.
Противолежащие углы параллелограмма равны (по свойству), значит угол C = угол A = 90°; угол D = угол B = 90°
Получили, что все углы параллелограмма прямые, следовательно, это по определению прямоугольник, ЧТД.