На стороне dk параллелограмма cdkm взята точка p так, что cd = dp. а) докажите, что cp – биссектриса - id945455020201114 от киря2289 14.11.2020 17:23

Question

Геометрия: На стороне dk параллелограмма cdkm взята точка p так, что cd = dp. а) докажите, что cp – биссектриса угла dcm. б) найдите периметр параллелограмма, если km = 16 cм, pk = 7 см.

киря2289 · Accepted Answer

В равнобедренном треугольнике углы при основании равны.

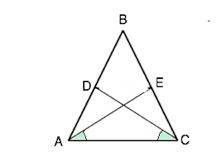
Рассмотрим ∆ ВСD и ∆ BAЕ. ∠АВС- общий.

∠ВАЕ=∠ВАС-∠САЕ,

∠ВCD=∠ВСА-∠АСD. По условию ∠ЕАС=∠DCА, ⇒ ∠ВАЕ=∠ВСD

Треугольники ВАЕ и ВСD равны по стороне ( АВ=ВС по условию) и прилежащим к ней углам (ВАЕ=ВСD, угол В - общий). Следовательно, ВD=ВЕ. Доказано.

* * *

Вариант решения- доказать равенство треугольников АСD и АСЕ по общей стороне АС и двум прилежащим углам. Тогда при вычитании из равных сторон АВ и СВ равных отрезковостанутся равные BD и ВЕ

Дан равнобедренный треугольник abc с основанием ac. точки d и e лежат соответственно на сторонах ab

На стороне dk параллелограмма cdkm взята точка p так, что cd = dp. а) докажите, что cp – биссектриса угла dcm. б) найдите периметр параллелограмма, если km = 16 cм, pk = 7 см.

MOGZ ответил