Задача
Дано:
периметр равностороннего треугольника 18 см
периметр равнобедренного треугольника 20 см
Сторона равностороннего треугольника является основанием равнобедренного треугольника
Найти: стороны равнобедренного треугольника
Решение
1) 18:3=6 (см) - сторона равностороннего треугольника;
2) пусть боковые стороны равнобедренного треугольника равны х см, тогда
х +х + 6 = 20
2х=20-6
2х=14
х=7 (см) - боковые стороны равнобедренного треугольника;
ответ: стороны равнобедренного треугольника равны 6 см, 7 см и 7 см.
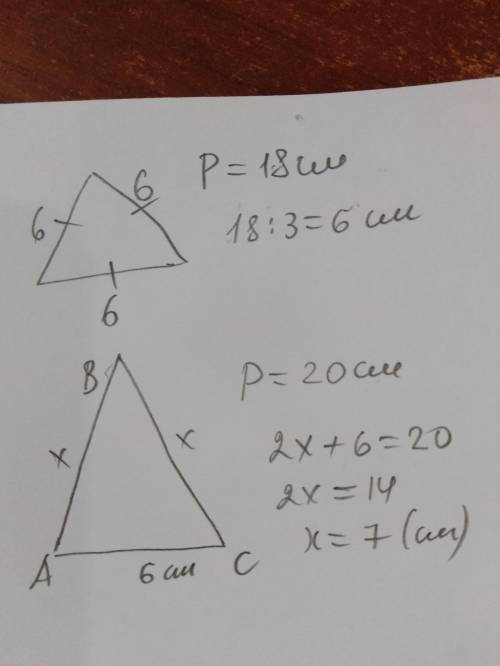
Стороны оснований правильной четырехугольной усеченной пирамиды относятся, как 3:2. Высота пирамиды равна 3. Боковое ребро составляет с плоскостью основания угол 60°. Найдите объем пирамиды .
Дано :
ABCDA₁B₁C₁D₁ _ правильная усеченная пирамида
AB = BC=CD=DA =a ; A₁B₁ = B₁C₁=C₁D₁=D₁A₁ =a
a : b =3 : 2 ; H =3 ; ∠A₁A0 = 60°
V - ?
V = (1/3)*( S₁ + √S₁S₂ + S₂)*h = [ a =1,5b , h=3 ] = (1/3)*3*( a²+ ab + b²)=
= (1,5b)²+ 1,5b*b + b² = 4,75b²
Остается вычислить b
AA₁C₁С - трапеция , проведем A₁H ⊥ AC ,∠A₁AH = 60°
AC = a√2 = 1,5b√2 ; A₁C₁ = b√2
AH = (AC - A₁C₁) /2 =( 1,5b√2 - b√2 ) /2 = 0,25√2*b
Из ΔAHA₁ : h =A₁H =AH*tg60° = 0,25√2*b*√3= 0,25√6 * b
b=h / 0,25√6 = 3 / 0,25√6 =4*3 /√6 =2√6
V =4,75b² =4,75*(2√6)² =4,75*4*6 =19*6 =114
ответ: 114 .
При пересечении двух прямых образуются вертикальные углы. Вертикальные углы равны. А также смежные, сумма которых 180°. Так как дана разница, рассматриваем смежные углы. Острый х, тупой х+42°, вместе 180°. Уравнение:
х+х+42=180,
2х=138,
х=138:2,
х=69° острый угол, вертикальный к нему также 69°.
69°+42°=111° тупой угол, вертикальный к нему 111°.
ответ: 69°, 69°, 111°, 111°.