Четырёхугольник ABCD - параллелограмм.
ВЕ = DF (Е ⊂ ВС, F ⊂ AD).
Доказать :Четырёхугольник AECF - параллелограмм.
Доказательство :В параллелограмме противоположные углы и противоположные стороны равны между собой (свойство параллелограмма).Отсюда следует, что ∠В = ∠D, АВ = CD.
Рассмотрим ΔАВЕ и ΔCDF.
ВЕ = DF (по условию)
∠В = ∠D, АВ = CD (по выше сказанному) ⇒ ΔАВЕ = ΔCDF по двум сторонам и углу между ними (первый признак равенства треугольников).
Из равенства треугольников следует и равенство сторон АЕ и CF.
AD = BC (по свойству параллелограмма), но в своё очередь AD = BE + EC ; BC = DF + AF. Учитывая равенство из условия получаем, что ЕС = AF.
Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник - параллелограмм (свойство параллелограмма).АЕ = CF ; ЕС = AF (по выше сказанному) ⇒ четырёхугольник AECF - параллелограмм.
ответ :Что требовалось доказать.
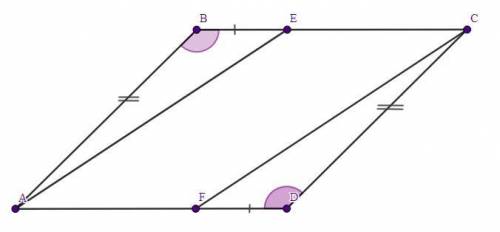
сделаем построение по условию
на рисунке осевое сечение шара и конуса (вертикальный разрез через вершину конуса)
r -радиус вписанной окружности, он же радиус шара вписанного в конус
r=3√2-3
треугольник АВС –равнобедренный, прямоугольный <ABC=90 град
<A=<C=45 град
BC1 - высота,биссектриса,медиана
<B1BO=<ABC1=90/2=45
OB1=r -перпендикуляр в точке касания
OС1=r -перпендикуляр в точке касания
треугольник B1BO –равнобедренный, прямоугольный < BB1O =90 град
BO=B1O / sin<B1BO =r / sin45 =(3√2-3) / 1/√2 =6-3√2
BC1=BO+OC1=6-3√2 +r =6-3√2 +3√2-3=3 - это высота пирамиды
треугольник ABC1 –равнобедренный, прямоугольный <AC1B =90 град
<A=<ABC1=45 град
AC1=BC1=3
AC1– это радиус основания
Площадь основания So= pi*AC1^2 = pi*3^2=9pi
Объем конуса V=1/3 *BC1 *So=1/3 *3 *9pi = 9pi =9п