рассмотрим треугольник АА1В,в нём, ВА1=5, т.к.в равнобедренном треугольнике медиана опущенная на основание является высотой.
В треугольнике найдём АА1=√169-25=12
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины
т.е АО=ВО, пусть АО=2х, тогда ОА1=2х, 2х+х=12, х=4.
АО=2*4=8
ВО=АО=8
ответ:8
1872шт.
Объяснение:
Для того чтобы узнать количество дощечек необходимо площадь пола поделить на площадь дощечки (обязательно чтобы площади были одинаковой ед. изменения, если пол в метрах, то и дощечки должны быть в метрах.)
Находим площадь пола (площадь прямоугольника равна произведению длины на ширину)
Sп.=11,7*4,8=56,16 м² площадь пола.
Переводим ед. измерения в одинаковую величину.
1м=100см.
30см=30/100=0,3 м
10см=10/100=0,1м .
Находим площадь дощечки.
Sд.=0,3*0,1=0,03 м² площадь дощечки.
Количество дощечек равно Sп/Sд.
56,16:0,03=1872 шт.
ответ 1872шт.
Обозначение:
Sп.- площадь пола
Sд.- площадь дощечки.
Иногда в таких задачах получается не целое число, тогда округлить нужно всегда в большую сторону. Например у вас получилось 1872,3, округлить в большую сторону 1873.
Объяснение:
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
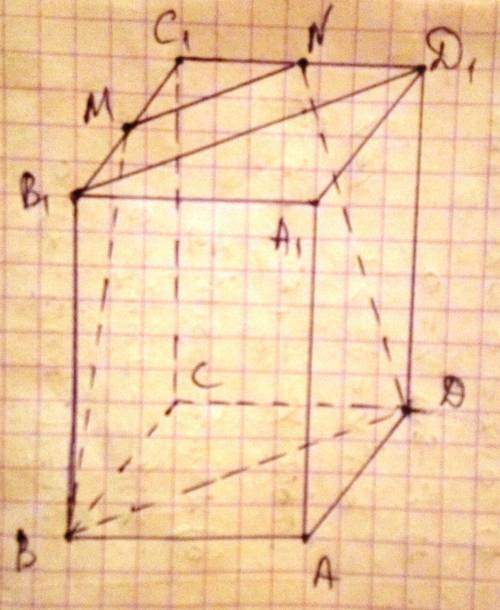
Пусть плоскость проведённая через B, D и серединную точку M ребра B₁C₁ пересекается с плоскостью B₁C₁А₁ по прямой MN. M∈B₁C₁, N∈D₁C₁.
⇒MN||BD⇒BDNM-трапеция
BD||B₁D₁; MN||BD⇒MN||B₁D₁
MN-средняя линия треугольника B₁C₁D₁
ABCDA1B1C1D1- правильный прямоугольный параллелепипед⇒ABCD-квадрат, а боковые грани прямоугольники.
B₁M=0,5B₁C₁=ND₁, DD₁=BB₁, ∠MB₁B=∠ND₁D=90°⇒ΔMB₁B=ΔND₁D⇒MB=ND⇒
⇒BDNM-равнобедренная трапеция. Ч.Т.Д.
BA1=0.5BC=5 cm (AA1- МЕДИАНА)
АО:ОА1=2:1 (МЕДИАНЫ ТОЧКОЙ ПЕРЕСЕЧЕНИЯ ДЕЛЯТСЯВ ОТНОШЕНИИ 2 К 1, СЧИТАЯ ОТ ВЕРШИНЫ)
ОА1=4 см
АА1 - высота треугольника, т. к. треугольник- равнобедренный
ОВ=( )=
)= cm
cm