АВ - произвольный отрезок.
1. Проведем луч с началом в точке А под произвольным углом к отрезку.
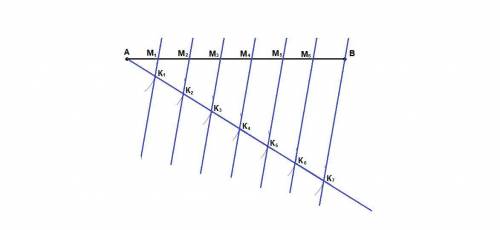
2. На луче от точки А с циркуля отложим 7 одинаковых отрезков произвольной длины:
АК₁ = К₁К₂ = К₂К₃ = К₃К₄ = К₄К₅ = К₅К₆ = К₆К₇
3. Проведем прямую К₇В через конец последнего отрезка и точку В.
4. Через точки К₁, К₂, К₃, К₄, К₅ и К₆ проведем прямые, параллельные прямой К₇В.
Точки пересечения этих прямых с отрезком АВ разделят отрезок АВ на 7 равных частей (по теореме Фалеса)
АМ₁ = М₁М₂ = М₂М₃ = М₃М₄ = М₄М₅ = М₅М₆ = М₆В
1) Друга висота дорівнює 24 см
Объяснение:
Маємо парал. АВСД АВ=8 см , ВС=16 см , ВК(висота до сторониАД) =12 см, знайти іншу висоту до сторони СД Можна через квадратне рівняння , а можна швидче, якщо порівняти подібні трикутники АВЕ і ВКС ВЕ/АВ=ВК/ВС ВК(друга висота)=12*16/8=24 см.
2)S=48²=2304 см²
3) Р=48 знайти площу нехай Х буде стороною квадрата , 4Х=48 , Х=12 S=12²=144 см²
4) позначимо сторону прямокутника через Х, друга буде 5Х , складемо периметр:2х+10х=44 12х=44 х=3,7 , друга сторона =5*3,7=18,5 S=18,5*3,7=68.5 см²
5) S =1/2*27*22=297 см²
6)S= 1/2*13*14=91см²
2 признак:по стороне и двум прилежащим к ней углам.
Это в кратце.