ответ: 7/8
Объяснение:
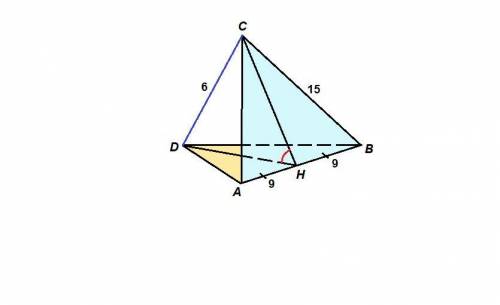
Пусть Н - середина АВ.
СН - медиана равнобедренного треугольника АВС, значит СН - высота, СН⊥АВ.
DH - медиана равнобедренного треугольника ABD, значит DH - высота.
DH⊥AB.
Следовательно, ∠CHD - линейный угол двугранного угла между плоскостями, искомый.
ΔСНВ: ∠СНВ = 90°, НВ = АВ/2 = 9; по теореме Пифагора
СН = √(СВ² - НВ²) = √(15² - 9²) = √(225 - 81) = √144 = 12
DH - медиана, проведенная к гипотенузе прямоугольного треугольника, значит равна половине гипотенузы:
DH = AB/2 = 9
Из ΔCHD по теореме косинусов:
CD² = CH² + DH² - 2 · CH · DH · cos∠CHD
36 = 144 + 81 - 2 · 12 · 9 · cos∠CHD
216 · cos∠CHD = 189
cos∠CHD = 189 / 216 = 7/8
1 вариант) S=1\2*AC*BC*Sin60°=1\2*12*8*√3\2=24√3 см²
2 вариант( без косинусов)
Из вершины И проведем BH⊥AC
ΔBHC-прямоугольный, ∠ACB=60°, ∠HBC=90°-60°=30°
Против угла в 30° лежит катет, равный половине гипотенузы, то есть HC=8\2=4 см
По теореме Пифагора найдем BH²=BC²-HC²=64-16=48
BH=√48=4√3 см
S=1\2*AC*BH=1\2*12*4√3=24√3 см²