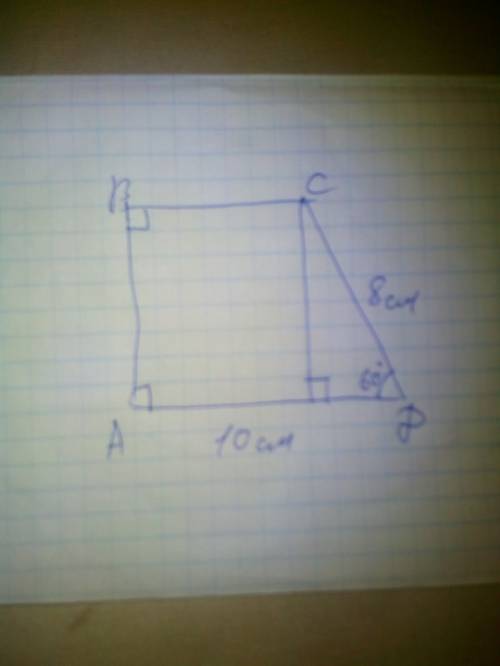
Нехай дано трапеція ABCD, AD=10см, CD=8см, кут D=60°, кутА=В=90°, проведемо з кута С висоту до AD точку перетину назвемо К, розглянемо прямокутний трикутник що утворився, кут КСD=90°-60°=30°, що означає КD=CD÷2=8÷2=4см
АВСК - прямокутник ( його кути по 90°) тоді ВС=АК=AD-KD=10-4=6см
Відповідь: 6см.
Можно пристроить к кубу ABCDA1B1C1D1 другой такой же куб следующим образом. Продлим ребра А1А, В1В, С1С, D1D за точки А,В,С,D. на длину ребра куба и через полученные точки A2,B2,C2,D2 проведем плоскость II АВС. Ясно, что я просто "приставил снизу" еще один куб, идентичный исходному.
Очевидно, что А2С II AC1, поэтому угол между СЕ и АС1 равен углу А2СЕ.
Замкнем треугольник А2СЕ, проведя А2Е в плоскости А2А1D1D2.
В треугольнике А2СЕ очень просто вычисляются все стороны.
A2C = √3; (это - диагональ куба, ребро принимаем за единицу длины, то есть ребро куба 1).
из прямоугольного тр-ка А2ЕD2 с катетами A2D2 = 1; D2E = 3/2; находим
А2Е = √(1^2+(3/2)^2) = √13/2;
аналогично из треугольника DCE
CЕ = √(1 + (1/2)^2) = √5/2;
Обозначим косинус угла А2СЕ как х. По теореме косинусов
13/4 = 3+5/4 - x*2*√(5*3)/2;
x = 1/√15 = √15/15; это - косинус искомого угла.
ABCD - трапеція, ВС||АD, <А=90°, АВ=8см, ВС=8см, СD=10см.
СК-висота. СК=АВ=8см.
АК=ВC=8см.
Δ СКD - прямокутний, тоді за теоремою Піфагора:
СК²+КD²=СD²=100-64=36
КD= (корінь)з 36 = 6 см
АD=АК+КD=8+6=14 (см)
S=h(a+b):2
S=8(8+14):2=22·4=88 (см²)