Будем считать, что задание дано так:
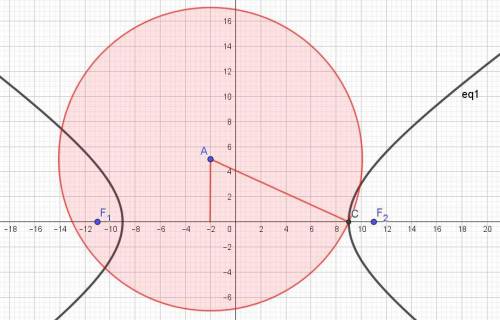
Определить уравнение окружности, проходящей через правую вершину гиперболы 40x² - 81y² = 3240 и имеющей центр в точке А(-2; 5).
Уравнение гиперболы приведём к каноническому виду, разделив обе части заданного уравнения на 3240:
(x²/81) - (y²/40) = 1.
Или так: (x²/9²) - (y²/(2√10)²) = 1 это и есть каноническое уравнение.
Отсюда находим координаты правой вершины гиперболы: С(9; 0).
Теперь находим радиус заданной окружности как отрезок АС.
АС = √((9 - (-2))² + (0 - 5)²) = √(121 + 25) = √146.
Получаем ответ: (x + 2)² + (y - 5)² = 146.
Сума величин кутів трикутника АОВ, що створюють діагоналі та одна сторона прямокутника завжди дорівнює 180 градуса, тобто:АВО+ВОА+ОАВ=180Гр.А і В є вершинами протилежних кутів пряокутника, що прилягають до однієї сторони. Отже у прямокутнику дані кути будуть однакові, тобто величина кута АВО=величині кута ВАО=30градусам. Звідси 180-30-30=120градусів -величина кута АОВ, що є кутом між діагоналяи прямокутника.
ДОДАТКОВО:Отже ми маємо два протилежні кути по 120гр. Сума величини кутів прямокутника становить 360 гр.Причому величини протележних кутів однакові. Маємо 360-120-120=120. 120/2=60. маємо кути: АОВ=СОД=120гр. ВОС=ДОА=60гр.
Пусть дан правильный треугольник АВС со стороной "а". Тода его площадь равна S=(√3/4)*a² (формула). Пусть дана точка М внутри треугольника таая, что МН=4см, МР=5см и МК=6см, где МН, МР и МК - перпендикуляры к сторонам АВ, ВС и АС соответственно или, что одно и то же, высоты треугольников АМВ,ВМС и АМС соответственно. Площадь треугольника АВС равна сумме площадей этих треугольников, то есть (1/2)*4*а+(1/2)*5*а+(1/2)*6*а = (√3/4)*а² => а = 7,5*4/√3.
Итак, сторона нашего треугольника равна 10√3. Тогда по приведенной выше формуле Sabc = (√3/4)*300 = 75√3 см².
ответ: Sabc= 75√3 см².