Луч - это часть прямой, лежащая по одну сторону от заданной точки, называемой началом луча. При именовании луча двумя буквами на первом месте всегда стоит название точки, обозначающей начало луча, на втором месте название любой другой точки луча.
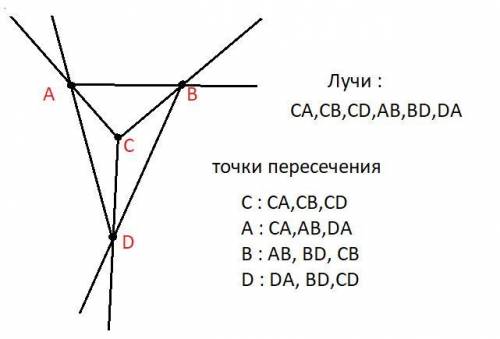
Лучи : CA, CB, CD, AB, BD, DA
Точки пересечения лучей:
C : CA, CB, CD
A : AB, CA, DA
B : BD, CB, AB
D : DA, CD, BD
Задача 22:
∠B=180°-∠ABD=180°-112°=68° - как смежные
ΔABC - равнобедренный (AB=BC), поэтому ∠A=∠C
∠A=∠C=(180°-68°):2=112°:2=56°
ответ: ∠A=∠C=56°
Задача 24:
ΔABC - равнобедренный (AC=BC), поэтому ∠A=∠B
∠A=∠B=(180°-75°):2=105°:2=52,5°
∠B=∠DBK=52,5° - как вертикальные
ответ: ∠DBK=52,5°
Задача 29:
∠DAB=180°-48°=132° - как смежные
ΔABD - равнобедренный (AD=AB), поэтому ∠BDA=∠ABD
∠BDA=∠ABD=(180°-132°):2=48°:2=24°
ΔCBE - равнобедренный (CB=CE), поэтому ∠CBE=∠CEB
∠CBE=∠CEB=56°
Отсюда ∠BCE=180°-56°*2=180-112°=68°
∠ACB=180°-∠BCE=180°-68°=112° - как смежные
∠ABC=180°-(∠ACB+∠BAC)=180°-(112°+48°)=180°-160°=20°
∠DBE=∠ABD+∠ABC+∠CBE=20°+24°+56°=100°
ответ: ∠DBE=100°, ∠D=24°
Задача 25:
∠DОC=180°-∠DОA=180°-137°=43°
∠DОC=∠AОB=43° - как вертикальные
ΔDОC - равнобедренный (DО=ОC), поэтому ∠D=∠C
∠D=∠C=(180-43°):2=68,5°
ΔAОB - равнобедренный (AB=АО), поэтому ∠AОB=∠В
∠AОB=∠В=43°
∠A=180°-43°*2=180°-86°=94°
ответ: ∠A=94°, ∠В=43°, ∠C=68,5°, ∠D=68,5°
Лучи:
A₁A₂, B₁B₂, C₁C₂, D₁D₂, E₁E₂, F₁F₂.
Через точки пересечения проходят по 3 луча:
1: C₁C₂, D₁D₂, E₁E₂ ;
2: A₁A₂, B₁B₂, E₁E₂ ;
3: B₁B₂, D₁D₂, F₁F₂ ;
4: A₁A₂, C₁C₂, F₁F₂ .