Поскольку угол В = 2 угла А, а биссетриса делит угол В пополам,
то уг. АВД = уг. А, и тр-к АВД -равнобедренный, т.е. ВД = АД.
В тр-ке АВД угол ВДА = 180° - 2уг.А, тогда в тр-ке ВСД угол ВДС = 2уг.А, а уг.ДВС = уг.АВД = уг.А т.к. ВД - биссектриса.
По теореме синусов для тр-ка ВСД:
200:125 = sin уг.2А : sin уг.А
1,6 = 2sin уг.А·cos уг.А : sin уг.А
1,6 = 2·cos уг.А
cos уг.А = 0,8, тогда sin уг. А = √(1 - 0,8²) = √(1 - 0,64) = √0,36 = 0,6
по теореме косинусов для тр-ка ВДС найдём его сторону (искомую биссектису) ВД
ДС² = ВС² + ВД² - 2·ВС·ВД·cos уг.А
125² = 200² + ВД² - 2·200·ВД·0,8
-24375 = - 320ВД + ВД²
ВД² - 320ВД + 24375 = 0
D = 102400 - 97500 = 4900
√D = 70
ВД₁ = (320 - 70):2 = 125
ВД₂ = (320 + 70):2 = 195
ответ: ВД₁ = 125, ВД₂ = 195
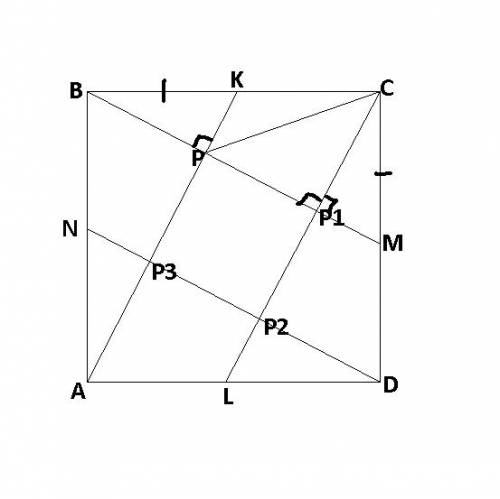
Условие: АВСD - квадрат, ВК=КС, СМ=MD, АК перес. ВМ = Р
Найти: угол СРМ
Решение: проведём прямые CL и DN так, что AL=LD, BN=NA. Поскольку АВСD - квадрат по условию, а точки К, L, M и N - середины сторон квадрата, то следовательно, CL паралл. AK, DN паралл. BM. Обозначим точки пересечения прямых через P1, P2, P3. Так как отрезки AK, CL, MB, DN попарно параллельны и являются раными отрезками внутри квадрата АВСD, то, следовательно, РР1Р2Р3 - также квадрат.
Так как мы провели аналогичные прямые уже проведённым, то, следовательно, и разделились они между собой в таком же отношении, как и прямые ВМ и АК, значит ВР=РР1, а так как РР1Р2Р3 - квадарат из решения, то Р1Р2=РР1 по определению квадрата, а также Р1Р2=СР1, значит СР1=Р1Р.
Рассмотрим треугольник СРР1, он прямоугольный, так как угол СР1Р смежный с углом квадрата РР1Р2, значит угол СР1Р=180-90=90 градусов. Помимо этого, треугольник СРР1 - равнобедренный, так как СР1=Р1Р, а в равнобедренном прямоугольном треугольнике углы при основании равны 45 градусов, значит угол СРМ=45 градусов.
ответ: 45 градусов.