Объяснение:
Дано:
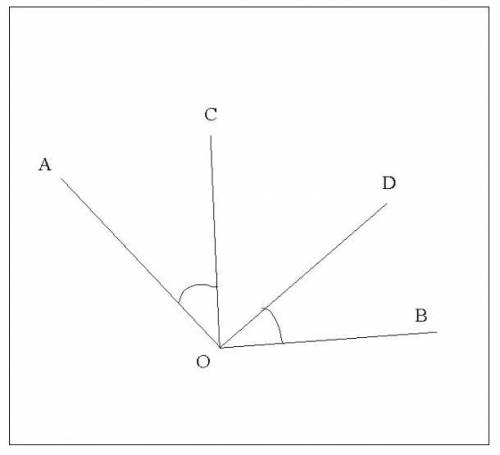
<AOB и <COD
<COD внутри <AOB
AO ┴ OD; CO ┴ OB;
<AOB - <COD = 90°
Найти: <AOB и <COD.
Решение
Т.к . AO ┴ OD; CO ┴ OB,
то <AOD = 90; <COB = 90°.
<COD = <AOD - <AOC
<COD = <COB - <DOB
<COD = 90° - <AOC
<COD = 90° - <DOB
Получим
<AOC = 90° - <COD
<DOB = 90° - <COD
Следовательно <AOC = <DOB
2) По условию: <AOB - <COD = 90°
Но если от всего угла <AOB отнять <COD, то останутся два равных угла <AOC и <DOB, значит, это их сумма равна 90°.
<AOC + <DOB = 90° =>
<AOC = <DOB = 90°/2 = 45°
3) <COD = 90° - <DOB
<COD = 90° - 45°=45°
4) <AOB = <AOC + <DOB + <DOB
<AOB = 45° + 45° + 45° = 135°
ответ: <AOB - 135°; <COD =45°.
Площадь полной поверхности конуса = сумма площади боковой поверхности и площади основания конуса.
Примем радиус основания равным r.
Тогда площадь основания πr²
Формула площади боковой поверхности конуса πrL. ⇒
Sбок=20πr
По условию πr²+πrL=400⇒⇒
3,14r²+60,28r-400=0
Решив квадратное уравнение, получим r1=5,16, r2 - отрицательный и не подходит.
r=5,16 см
Площадь боковой поверхности πrL=S=π•5,16•20=103,2π - площадь меньшего сектора круга радиусом 20 см
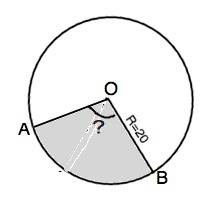
Площадь сектора АОВ=πR²α :360° , где R=L=20 см, α- угол развертки конуса.
π•400•α :360°=103,2π, откуда α=92,88°° = или ≈ 92°53'.
Исходя из условий высота равна 19,6 см (12+7,6)
12/2 = 6
Теперь по формуле 6 * 19,6 = 117,6