Дано: ABCD - трапеция
AM = MB
CP = PD
BC // MP // AD
MP = 3
BC = 5
Найти: AD
MP - средняя линия трапеции ABCD ( по определению средней линии: отрезок, соединяющий середины боковых сторон трапеции, называется средней линией этой трапеции )
Длинна средней линии находится по формуле ⇒ 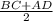
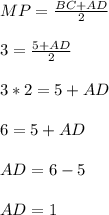
ответ: AD = 1
P.s - мне кажется, правильнее было бы верхнее основанее назвать AD, а нижнее BC ( так как верхнее основанее не может быть больше средней линии, а нижнее не может быть меньше)
⇒ фото чтобы вы поняли, что я имею ввиду
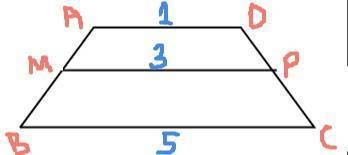
Я знаю первое))
Дано:тр-к АВС,АВ=ВС=17,ВД-высота_cosA=8/17 Найти:ВД Pешение: 1)cosA=AD/AB=>8/17=AD/17=>AD=8. 2)BD²=AB²-AD²;BD²=17²-8²=(17-8)(17+8)=9*25=>BD=3*5=15.
А второе только без дано((
Пусть высота проведенная к большей стороне(АД) - ВН. Площадь параллелограмма равна произведению основания на высоту проведенную к этому основнию, значит S=BH*AD=14*4=56(см)^2-площадь параллелограмма.
Обозначим вторую высоту проведенную к стороне СД, как АК, тогда по формуле площади парллелограмма имеем:
S=AK*CD, отсюда АК=S/CD=56/8=7(см).
ответ: 56см^2, 7см.
Это задачи на применение теоремы Пифагора: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов, т.е.: с² = а² + b², где a и b - катеты, c - гипотенуза.
1. а = 9, b = 12, тогда с² = 9² + 12² = 81 + 144 = 225 = 15², откуда с = 15.
ответ: 15.
2. а = 12, с = b + 8. Найдем b и с.
По теореме Пифагора получим: 12² + b² = (b + 8)²,
144 + b² = b² + 16b + 64,
-16b = 64 - 144,
-16b = -80,
b = 5.
Тогда с² = 12² + 5² = 144 + 25 = 169 = 13², откуда с = 13.
ответ: 13.
3. с = 26, а = 10. Найдем S.
Из теоремы Пифагора найдем второй катет: b² = с² - а² = 26² - 10² =
= 676 - 100 = 576 = 24², откуда b = 24.
Площадь прямоугольного треугольника находят по формуле:
S = 1/2 · а · b, где а и b - катеты, S - его площадь.
Теперь S = 1/2 · 10 · 24 = 120.
ответ: 120.