Втреугольнике авс ав = вс. на сторонах ав и св соответственно выбраны точки а1 и с1 так, что

Question

Геометрия: Втреугольнике авс ав = вс. на сторонах ав и св соответственно выбраны точки а1 и с1 так, что

murad2097 · Accepted Answer

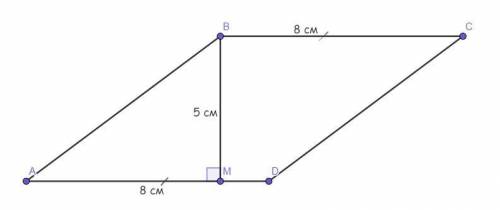
У параллелограмма ABCD проведена высота ВМ к стороне AD. Найдите площадь этого параллелограмма, если ВС = 8 см, ВМ = 5 см.

▔ ▔ ▔

★☆★ Чертёж смотрите во вложении ★☆★

Дано:

Четырёхугольник ABCD — параллелограмм.

ВМ — высота, опущенная на сторону AD = 5 см.

ВС = 8 см.

Найти:

S(ABCD) = ?

Решение:

▸Противоположные стороны параллелограмма равны◂

AD и ВС — противоположные стороны.

Следовательно, по выше сказанному —

AD = ВС = 8 см.

▸Площадь параллелограмма равна произведению стороны и высоты, опущенной на эту сторону◂

Следовательно —

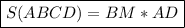
$\boxed{S(ABCD) =BM* AD}$

Подставим в формулу известные нам значения в формулу —

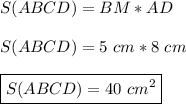$S(ABCD) =BM*AD\\\\S(ABCD)=5 \ cm*8\ cm\\\\\boxed{ S(ABCD)=40\ cm^{2} }$ ответ:

40 см².