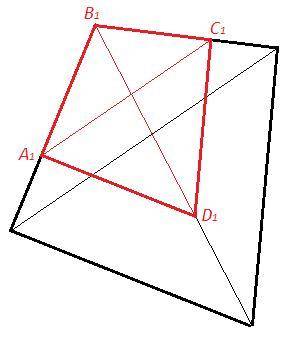
Соответствующие диагонали разбивают подобные многоугольники на подобные треугольники.
Доказываем подобие треугольников (с одинаковым коэффициентом и соответствием сторон) - тем самым доказываем подобие многоугольников.
(3) A1B1C1~ABC, A1D1C1~ADC (по двум сторонам и углу между ними)
(4) A1B1C1~ABC (по данным смежным сторонам и углу между ними)
A1D1C1~ADC (по стороне (A1C1, AC) и прилежащим углам)
(6) A1B1C1~ABC, A1B1D1~ABD (по трем пропорциональным сторонам)
∠C1A1D1=∠CAD
C1A1D1~CAD (по двум сторонам и углу между ними)
Итак, есть выпуклый многоугольник. как подсчитать , сколько диагоналей можно провести из одного угла? Этот угол не в счет. Значит, "минус один". К соседним двум тоже не проведешь диагональ, т.к. это будут стороны. Значит, еще минус два. Итого минус три . к остальным проводятся. Т.е. у такого n-угольника можно из каждого угла провести (n-3) диагонали, а таких углов n? тогда диагоналей будет n*(n-3)
но некоторые начинают повторяться . С 1-го и 2-го угла можно провести n-3, с 3-го n-4 и т.д. до n-2 угла. С него проводится только 1 диагональ. Т.е. считая с конца, можно провести 1+2+3+...+(n-3) (это со 2-го угла) + (n-3) (это с первого) . Получается арифметическая прогрессия S=
где n-кол-во углов
у нас n=15+3=18
тогда диагоналей 135
вроде так