1)
или вот рисунок
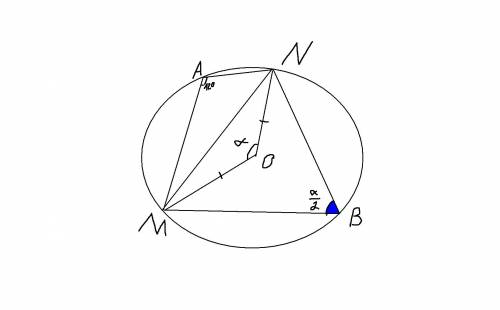
Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равна 180 , возьмем такую точку А на меньшей дуге, и на большой точку В , углы AMB+ANB=180 гр , угол В = 180-120=60
угол NBM вписанный и равен половине центрального то есть 120 гр, и через равнобедренный треугольник NOM
найдем по теореме косинусов MN
MN^2 =2*8^2-2*8^2*cos120
MN=√192 = 8√3
2)
площадь ромба
S=d1*d2/2
стало 1.1d1 , другая 0.85d2
S=1.1*0.85*d1*d2/2 = 0.935*d1*d2/2
то есть 1-0,935 = 0,065 уменшиться на 6,5 %
"Вспоминаем" подходящие формулы.
Радиус окружности, вписанной в равнобедренный тр-к:
r = b/2* √(2a-b)/(2a+b), где b - основание, а - боковая сторона.
b = 2aCosα, где b - основание, а - боковая сторона, α - угол между ними.
Площадь S=1/2*a*b*Sinα
Вставляем известные величины: r = (2aCosα/2)*√(2a-2aCosα)/(2a+2aCosα) =
aCosα√[(1-Cosα)/(1+Cosα)]. Тогда а=r/(Cosa*√[(1-cosa)/(1+cosa)])=r/(cosa√[sin^2a/(1+cosa)^2]=r(1+cosa)/(cosa*sina).
b = 2a*Cosa
S = (1/2)*a*b*Sina=(1/2)*r(1+cosa)*2a*cosa*sina)/(cosa*sina)=r(1+cosa)*r*(1+cosa)/(cosa*slna) = r^2*(1+cosa)^2/(cosa*sina)=r^2*(1+2cosa+cos^2a)/(cosa*sina).
Sin30=1/2. Cos30=√3/2. Тогда
S=r^2*4*(4+4√3+3)/(√3*4)=r^2*(7+4√3)/√3 = 8,005*r^2 =~8r^2.
ответ: S = 8r^2.