64 см²
Объяснение:
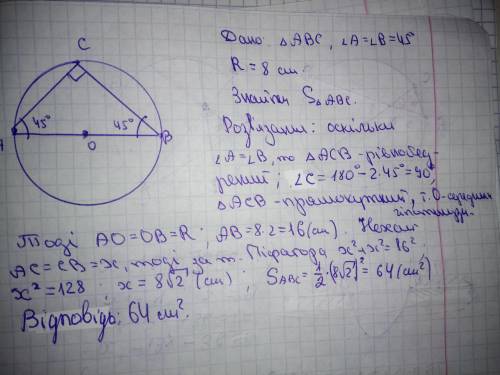
Радиус R окружности, описанной около треугольника, связан с его стороной a соотношением:
R = а/(2sinα), где α - угол, который лежит против стороны a.
Пусть α - углы при основании, равные 45°.
Тогда боковая сторона а равна:
а = R · (2 sinα) = R · (2 sin 45) = 8 · 2 · (√2/2) = 8√2 см.
Площадь треугольника равна половине произведения его сторон на синус угла между ними.
Между равными боковыми сторонами лежит угол:
180 - 45 - 45 = 90°.
Отсюда площадь треугольника равна:
(8√2 · 8√2 · sin 90°) : 2 = (64 · 2 · 1) : 2 = 64 см²
ответ: 64 см²
149,09 см²
Объяснение:
1) Зная ∠В (80°) и противолежащую этому углу сторону (NT = 25 см), найдём радиус R описанной окружности:
R = NT : (2 · sin 80°) = 25 : (2 · 0,98480775) ≈ 25 : (2 · 0,9848) = 25 : 1,9696 = 12,6929326 ≈ 12,6929 см.
2) Находим угол Т:
∠Т = 180° (сумма внутренних углов треугольника) - 30° - 80° = 70°.
3) Зная радиус описанной окружности (R = 12,6929 см) и ∠Т (70°), находим сторону NB, противолежащую углу Т:
R = NB : (2 · sin ∠Т)
R = NB : (2 · sin 70°)
NB = R · (2 · sin 70°) = 12,6929 · 2 · 0,93969262 ≈ 12,6929 · 2 · 0,9397 = 23,855036 ≈ 23,8550 см
3) Находим площадь треугольника NBT как половину произведения сторон NT (25 см) и NB (23,8550 см) на синус угла N между ними:
SNBT= (NT· NB · sin ∠N) : 2 = (25 · 23,8550 · sin 30°) : 2 = (596,375 · 0,5) : 2 = 298,1875 : 2 = 149,09375 ≈ 149,09 см².
ответ: площадь треугольника NBT равна 149,09 см².
ответ: M(3;2) и N(0;4)
Пошаговое решение:
1) По условию отрезок AB должен быть параллелен отрезку MN. Значит, их точки имеют одну общую координату с соответствующей точкой на отрезке, параллельном данному и одну различающуюся.
2) Составим линейную функцию для прямой, которой принадлежат точки A и B. Так как точка A находится ниже точки B, коэффициент линейной функции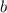 будет отрицательным: прямая пойдёт вниз по оси Y.
будет отрицательным: прямая пойдёт вниз по оси Y.
3) Найдём коэффициент линейной функции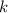 по формуле:
по формуле:
4) Так как точки C, M и N коллинеарны, они принадлежат одной прямой. Это значит, что прямая с точками C, M и N должна вся быть параллельная прямой с точками A и B. Значит, у этих двух прямых будет одинаковый коэффициент наклона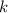 .
.
5) Точка M будет находиться над точкой A по оси Y, точка N будет находиться над точкой B по оси Y. Зная координаты точки C и коэффициент наклона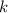 , можно рассчитать координаты точек M и N.
, можно рассчитать координаты точек M и N.
6) Рассчитаем координаты точки M:
7) Рассчитаем координаты точки N:
По коэффициенту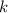 доказываемо, что эти координаты справедливы: сдвинувшись на 3 влево по x, получим координату x для точки M, равную 3, а поднявшись на 2 вверх по y, получим координату y для точки M, равную 2. Сдвинувшись на 3 влево по x от точки M, получим координату x для точки N, равную 0, а поднявшись на 2 вверх по y, получим координату y для точки N, равную 4.
доказываемо, что эти координаты справедливы: сдвинувшись на 3 влево по x, получим координату x для точки M, равную 3, а поднявшись на 2 вверх по y, получим координату y для точки M, равную 2. Сдвинувшись на 3 влево по x от точки M, получим координату x для точки N, равную 0, а поднявшись на 2 вверх по y, получим координату y для точки N, равную 4.