A6.
Сумма углов треугольника 180°. Если один угол тупой, то есть больше 90°, то два других в сумме не могут быть больше или раны 90°.
Следовательно, другие два угла всегда будут острыми.
ответ: а) только острыми.
В1.
Прямоугольный треугольник — треугольник, у которого один из углов 90°
ответ: KMN, ∠M=90°; LHS, ∠H= 90°
B2. Против меньшей стороны треугольника лежит меньший угол. Определим же его:
∠ABC = 180−62 = 118°
∠A = 180−(118+40) = 180−158 = 22°
∠A — наименьший из углов Δ. Против него лежит сторона BC.
ответ: ВС.
Отрезок AC виден из точки B под данным углом - точка B лежит на некоторой данной дуге.
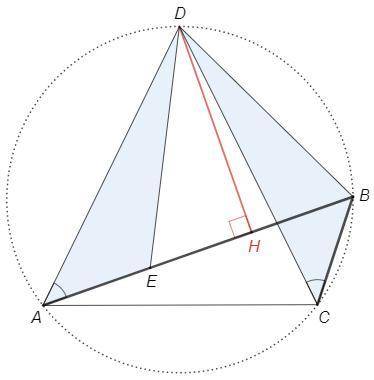
Задача Архимеда о половине ломаной:
Ломаная A-B-C вписана в дугу ADC, точка D - середина дуги. Докажем, что перпендикуляр DH, опущенный на больший отрезок AB, делит ломаную пополам.
Пусть AE=BC
DA=DC (стягивают равные дуги)
∠DAB=∠DCB (опираются на одну дугу)
△DAE=△DCB => DE=DB
△EDB - р/б, DH - высота и медиана, EH=HB
AE+EH=HB+BC
Теперь видно, что достаточно максимизировать отрезок AH.
В треугольнике ADH катет AH всегда меньше гипотенузы AD. Максимум достигается, когда точки H, D, B совпадают.
То есть, когда B - середина дуги, BA=BC.
.................................................