Будем использовать следующие значения для сторон треугольника АВС: АВ=с, ВС=а, СА=b и его углов:
<А=а, <В=b, <C=y (a, b, y : Альфа, Бэта, Гама.)
Дано:
а=4, b=5, c=6.
Найти: a, b, y -?
Пусть b - наибольшая сторона, b<a+c.
По теореме косинусов находим наибольший угол b,
[Не обязательно писать, для ориентира: Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.]
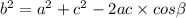
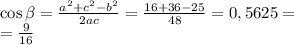
При основного тригонометрического тождества найдём Sin B
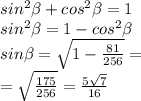
С теоремы синусов найдём углы треугольника:
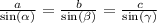
Отсюда,
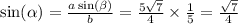
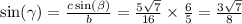
С таблиц находим градусную меру углов:
а≈41°
b≈57°
Тогда,
у≈82°
ответ: 41° 57° 82°
1)Треугольник МNK- равнобедренный.
Значит, углы при его основании равны => <NMK=<NKM=60°.
2)NP- медиана равнобедренного треугольника MNK, а значит, является одновременно биссектрисой и высотой. =>
3)Биссектриса NP делит угол N пополам. Поскольку угол N=60° (Сумма углов треугольника равна 180° => N = Треугольник MNK-M-K =180°-60°-60° = 60°), то <PNM= <PNK=30°.
4) NP - высота, а значит <NPM= <NPK=90°
Из этого следует, что треугольник NPK= <NPK+<PNK+<NKP= 90°+60°+30°
0,6 м
Пояснения:
Пусть АВ - шлагбаум.
АС = 1 - короткий конец, ВС = 3 - длинный конец.
Пошаговое объяснение:
При подъеме точка В переместится в В1, а - в А1 соответственно.
Проведем к АВ из точек В1 и А1 перпендикуляры, обозначим их концы точками В2 и А2 соответственно.
В прямоугольном треугольнике СВ1В2 sinC = B1B2 / CB1
В прямоугольном треугольнике СА1А2 sinC = A1A2 / CA1
Углы эти равны, как вертикальные, значит и их тангенсы равны.
значит B1B2 / CB1 = A1A2 / CA1
CB = CB1 = 3
СА = СА1 = 1
В1В2 = 1,8
Из пропорции получаем, что А1А2 = 1,8 х 1 / 3 = 0,6