a = 5 см,
b = 4 см,
c = 7 см.
Найти R.
Запишем теорему синусов:
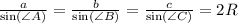
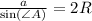
числитель и знаменатель дроби слева последнего равенства домножим на (b·c).
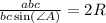
С учётом того, что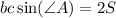 
, где S - площадь данного в условии треугольника, имеем
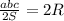
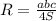
Площадь треугольника можно найти по формуле Герона:
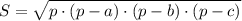, где
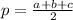
Найдем, сначала, площадь треугольника.
p = (5+4+7)/2 = (9+7)/2 = 16/2 = 8 см.
S = √(8·(8-5)·(8-4)·(8-7)) = √(8·3·4·1) = 4·(√6) см²
Теперь найдем радиус описанной окружности.
R = 5·4·7/(4·4·(√6)) = 5·7/(4·(√6)) = 35·(√6)/(4·6) = 35·(√6)/24 см.
Теперь найдём длину окружности, описанной около данного треугольника.
L = 2πR = 2π·35·(√6)/24 см = π·35·(√6)/12 см.
ответ: 5√4,32
Объяснение: проведём высоту к стороне 5 см. У нас получился прямоугольный треугольник, при котором угол равен 60° и прилежащая сторона 2,4. Верхний угол прямоугольного треугольника, который образовала высота равен: 180-90-60=30°. Катет, который лежит напротив угла 30° = половине гипотенузы. Гипотенуза 2,4. Поэтому 2,4÷2=1,2. Это первый катет. Теперь найдём высоту. По теореме Пифагора: 2,4(в квадрате)-1,2(в квадрате)=√4,32. Теперь найдём площадь: S=5×√4,32=5√4,32
Вы можете извлечь корень, у меня сейчас нет такой возможности
xₐ = (- 6 - 8) : 2 = -7; yₐ = (3 + (-1)) : 2 = 1; A(-7, 1);
Длина медианы DA = √x² + y² =√ 49 + 1 = √50 = 5√2