(МН·РН) = 4 ед.
(ОР·РК) = -2 ед.
Объяснение:
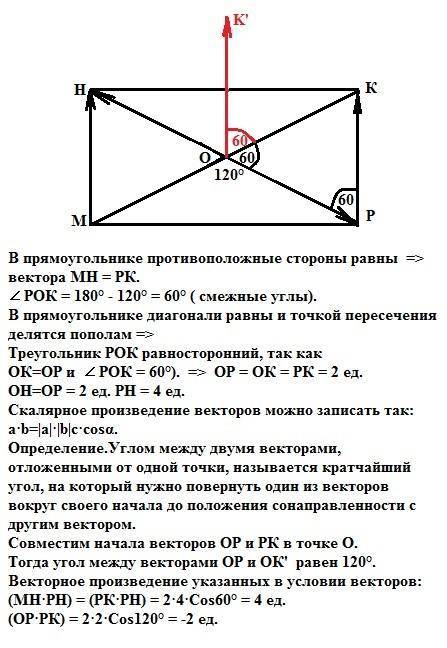
В прямоугольнике противоположные стороны равны =>
вектора МН = РК.
∠ РОК = 180° - 120° = 60° ( смежные углы).
В прямоугольнике диагонали равны и точкой пересечения делятся пополам =>
Треугольник РОК равносторонний, так как
ОК=ОР и ∠ РОК = 60°). => ОР = ОК = РК = 2 ед.
ОН=ОР = 2 ед. РН = 4 ед.
Скалярное произведение векторов можно записать так:
a·b=|a|·|b|c·сosα.
Определение: "Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором".
Совместим начала векторов ОР и РК в точке О. Тогда угол между векторами ОР и ОК' (вектора ОК и ОК' равны) равен 120°.
Векторное произведение указанных в условии векторов:
(МН·РН) = (РК·РН) = 2·4·Cos60° = 4 ед.
(ОР·РК) = 2·2·Cos120° = -2 ед.
объясняется предоставлением так называемых дешeвыx (или «удобных» , «подставных» ) флагов. Их называют также флагами открытой регистрации.
«Удобный» флаг – это национальный флаг какой-либо небольшой, как правило, страны, под которым ходит судно, зарегистрированное в ней, хотя его владельцем является гражданин другой страны. Это флаг страны, которая за умеренную плату заносит в свой реестр суда, принадлежащие собственникам из любых стран. «Удобный» флаг удобен государству, которое его предоставляет: оно без больших затруднений получает доход в виде платы за регистрацию и иные услуги.
Первой ввела льготный режим приписки судов в 1925 г. Панама. Ее примеру в 1948 г. последовала Либерия, а позднее и многие другие страны. Признанными странами удобного флага являются Антигуа и Барбуды, Багамы, Белиз, Бермуды, Кайманы, острова Кука, Кипр, Гибралтар, Гондурас, Ливан, Либерия, Мальта, Маршалловы острова, Маврикий, Нидерландские Антильские острова, Панама, Сент-Винсент и Гренадины, Шри Ланка, Тувалу и Вануату.