Дано :
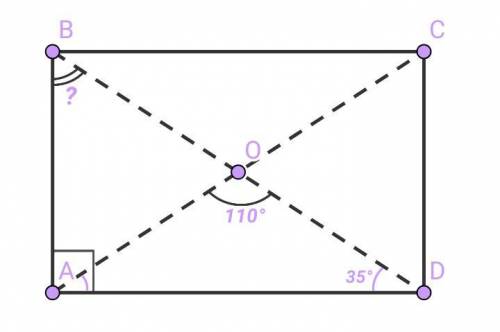
Четырёхугольник ABCD —прямоугольник.
Отрезки АС и BD — диагонали.
Точка О — точка пересечения диагоналей.
Угол AOD = 110°.
Найти :
Угол ABD = ?
Рассмотрим треугольник AOD.
Диагонали прямоугольника точкой пересечения делятся пополам и равны.
Следовательно —
АО = OD.
Тогда треугольник AOD — равнобедренный.
У равнобедренного треугольника углы у основания равны.
Следовательно —
Угол OAD = угол ODA.
По теореме о сумме углов треугольника —
Угол ODA = 0,5*(180° - угол AOD) = 0,5*(180° - 110°) = 0,5*70° = 35°.
Рассмотрим треугольник BAD — прямоугольный (так как угол BAD = 90° по определению прямоугольника).
Сумма острых углов прямоугольного треугольника равна 90°.
Следовательно —
Угол ABD = 90° - угол BDA
Угол ABD = 90° - 35° = 55°.
55°.
№2 конус АВС, В-вершина, О-центр основания, АО=радиус=R, уголВАО=30, АВ-образующая, треугольник АВО прямоугольный, ВО-высота конуса, АВ=АО/cos30=R/корень3/2=2R*корень3/3, ВО=1/2АВ=2R*корень3/6=R*корень3/3 =диаметр шара, объем конуса=1/3пи*радиус в квадрате*высота=(пи*R в квадрате*R*корень3)/(3*3)=пи*R в кубе*корень3/9, объем шара=4/3пи*радиус в кубе, радиус шара=R*корень3/6, объем шара=4/3пи*(R*корень3/6) в кубе=пи*R в кубе*корень3/54, объем конуса/объем шара=(пи*R в кубе*корень3/9) / (пи*R в кубе*корень3/54)=6/1
№3 диаметр цилиндра=высота цилиндра=2R, радиус цилиндра=R, объем цилиндра=пи*радиус в квадрате*высота=пи*R*R*2R=2пи*R в кубе, радиус шара=1/2высота цилиндра=2R/2=R, объем шара=4/3пи*радиус в кубе=4/3пи*R в кубе, объем цилиндра/объем шара=(2пи*R в кубе)/(4/3пи*R в кубе)=3/2