Если две прямые на плоскости перпендикулярные одной и той же прямой, то они параллельны. ⇒ а║b
Действительно: соответственные, внутренние и прочие углы при пересечении прямыми а и b прямой р равны.
Если некая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую.
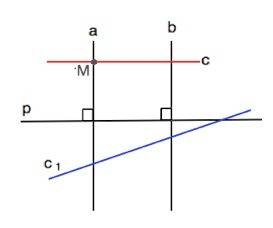
Пусть прямая с пересекает прямую а в точке М.
Допустим, что с не пересекает b. Тогда через точку М проходят две прямые, которые параллельны прямой b, что противоречит аксиоме
( В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой).
Заметим, что прямая с может быть параллельной прямой р или пересекать её ( на рисунке это с1).
Если две прямые на плоскости перпендикулярные одной и той же прямой, то они параллельны. ⇒ а║b
Действительно: соответственные, внутренние и прочие углы при пересечении прямыми а и b прямой р равны.
Если некая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую.
Пусть прямая с пересекает прямую а в точке М.
Допустим, что с не пересекает b. Тогда через точку М проходят две прямые, которые параллельны прямой b, что противоречит аксиоме
( В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой).
Заметим, что прямая с может быть параллельной прямой р или пересекать её ( на рисунке это с1).

х -высота из В на АД
Sавсд=х*АД=30 см²
Sавд=0,5х*АД=15 см²
Sавм=0,5х*ВМ=0,5х*0,5ВС=0,5х*0,5АД=0,25х*АД=7,5 см²
ΔОВМ подобен ΔОАД (по 3 углам)
Sоад=4Sовм (АД/ВМ=2, стороны в 2 раза S в 4)
Sавм-Sовм=Sавд-Sоад=Sавд-4Sовм
Sовм=(15-7,5)/3=2,5 см²
Sомсд=Sавсд-Sавд-Sовм=30-15-2,5=12,5 см²