Вычисли третью сторону треугольника, если две его стороны соответственно равны 4 см и 8 см, а угол между ними равен 120°. ответ: третья сторона равна ?
Для решения этой задачи мы можем воспользоваться теоремой косинусов. Эта теорема связывает длины сторон треугольника с косинусами углов, образованных этими сторонами.
Теорема косинусов имеет следующий вид:
c^2 = a^2 + b^2 - 2ab*cos(C)
Где c - третья сторона треугольника, a и b - две известные стороны, C - угол между этими сторонами.
В нашем случае, известны стороны a = 4 см и b = 8 см, а угол C = 120°. Нам нужно найти длину третьей стороны c.
Подставим известные значения в формулу теоремы косинусов:
c^2 = 4^2 + 8^2 - 2 * 4 * 8 * cos(120°)
Выполним вычисления.
Сначала найдем cos(120°). Для этого мы можем воспользоваться известным фактом, что cos(120°) = cos(360° - 120°) = cos(240°). Угол 240° лежит в третьем квадранте, где косинусы отрицательны, поэтому cos(240°) = -cos(60°). А cos(60°) = 1/2. Поэтому cos(120°) = -1/2.
Теперь подставим известные значения:
c^2 = 4^2 + 8^2 - 2 * 4 * 8 * (-1/2)
Продолжим вычисления:
c^2 = 16 + 64 + 64 = 144
Теперь найдем корень из полученного значения:
c = sqrt(144)
c = 12 см
Таким образом, третья сторона треугольника равна 12 см.
ответ: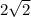 см.
см.