В основании правильной пирамиды - правильный треугольник. Вершина S проецируется в центр О основания. Высота правильного треугольника СН= (√3/2)*а, где а - сторона треугольника. СН=13√3/2. В правильном треугольнике высота=медиана и делится центром в отношении 2:1, считая от вершины. => HO=(1/3)*CH, а СО=(2/3)*СН или СО=13√3/3, НО=13√3/6.
По Пифагору:
Боковое ребро пирамиды SC=√(CO²+SO²) = √(313/3).
Апофема (высота боковой грани) SH=√(НO²+SO²) = √(745/12).
Боковая поверхность Sбок = (1/2)*3*АВ*SH =(39/4)*(√(745/3).
Відповідь:
3 см
Пояснення:
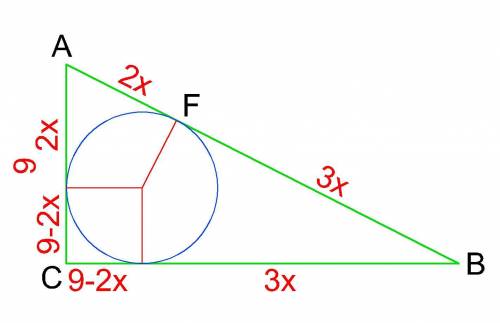
Відомо, що коло, вписане в трикутник, точками дотику до сторін відділяє рівні відрізки зі сторони кожної вершини.
Також відомо, що висоти - радіуси, проведені із центра такого кола в прямокутному трикутнику до катетів утворюють з відрізками від точок дотику до вершини прямого кута квадрат зі стороною, рівною радіусу вписаного кола.
Згідно з умовою, позначимо AF як 2x, FB як 3x, тоді
r=9-2x
За теоремою Піфагора складемо рівняння:
9²+ (9-2х+3х)²=(2х+3х)²
81+(9+х)²=25х²
81+81+18х+х²-25х²=0
24х²-18х-162=0
4х²-3х-27=0
Дискрімінант: Д=9+4*4*27=441=21²
х₁=(3+21)/8=3 см
х₂=(3-21)/8=-2.25 см (не підходить).
Тоді r=9-2·3=3 см
а) √7 ед. и 3√7 ед.
б) AD = (2√3+√19) ед.
в) R = (4√21)/3 ед.
Объяснение:
а) Найдем сторону ВС по теореме косинусов:
ВС = √(АВ²+АС² - 2·АВ·АС·Cos60) = √(16+144-48) = 4√7.
Биссектриса делит противоположную сторону в отношении, равном отношению прилежащих сторон, то есть:
Один отрезок (BD) равен 4√7·4/16 = √7 ед.
(так как ВС = 4х+12х = 16х).
Второй отрезок (CD) равен 4√7·12/16 = 3√7 ед.
б) По теореме косинусов в треугольнике ABD:
BD² = AB²+AD² - 2·AB·AD·Cos30 =>
7 = 16+AD²- 4·AD·√3 =>
AD²- 4·√3·AD -7 = 0. =>
AD = (2√3+√19) ед.
Второй корень отрицательный и не удовлетворяет условию.
в) R = a·b·c/4S. S = (1/2)·4·12·Sin60 = 12√3 ед².
R = 4·12·4√7/(48√3) = (4√21)/3 ед.