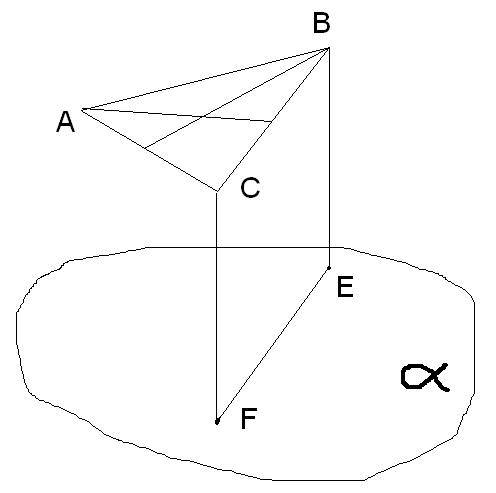
Поскольку в данном случае треугольник - фигура плоская, то все его медианы лежат в плоскости треугольника. И если две медианы параллельны плоскости альфа, то и треугольник параллелен этой плоскости. Таким образом, прямая ВС параллельна плоскости альфа. Поскольку прямые, проведенные из В и С параллельны между собой, то расстояние между точками Е и F на плоскости альфа будет равно расстоянию между В и С в плоскости треугольника. А так как плоскость треугольника параллельна плоскости альфа, то ВС будет параллельна ЕF. Длины параллельных прямых проведенных из В и С будут равны между собой, поскольку они проходят между двумя параллельными плоскостями (плоскостью альфа и плоскостью треугольника) Мы получили, что в четырехугольнике противоположные стороны попарно равны и параллельны. Значит этот четырехугольник параллелограмм.
О((-4+3)/2; (1-2)/2; (5+1)/2) или О(-0,5;-0,5:3). Теперь, зная координаты середины диагонали BD (точки О), находим координаты ее конца (точки D):
(Х-5)/2 = -1/2, значит х=4
(Y+4)/2=-1/2, значит y=-5
(Z+2)/2=3, значит z=4.
Итак, ответ: D(4;-5;4)