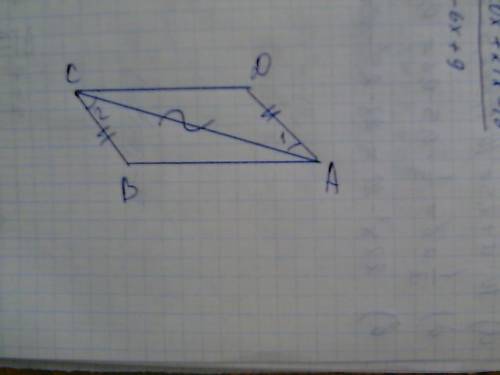
Как известно, диагонали точкой пересечения делятся пополам, а противоаоложные стороны пар-мма равны. Следовательно, противоположные по отношению друг к другу треугольники равны(по 3-ему признаку равенства треугольников), и площади их тоже равны.
Осталось доказать, что площади двух "смежных" треугольников равны. Рассмотрим их. Одна сторона у них общая, примем за основание сторону, лежащую на диагонали. Эти стороны у треугольников равны, т.к. точкой пересечения, повторюсь, диагонали делятся пополам. Прощадь треугольника у нас равна половине основания, умноженного на высоту, проведенную к основанию. Проведи к основаниям треугольников высоту - это будет один и тот же отрезок.
Мы получили - основания у треугольников равны, высоты равны.
Теорема доказана.
1) Проекция бокового ребра на основание - это половина диагонали квадрата основания.
То есть: d = 2*12*cos 60° = 24*(1/2) = 12 см.
Сторона основания а = d/√2 = 12/√2 = 6√2 см.
Площадь основания So = a² = 72 см².
Высота пирамиды равна: Н = 12*sin 60° = 12*(√3/2) = 6√3 см.
Объём пирамиды V = (1/3)SoH = (1/3)*72*6√3 = 144√3 см³.
2) Проекция апофемы на основание - это (1/3) высоты основания.
Тогда высота основания h = 3*(Н/tg 60°) = 3*(2√3)/(√3) = 6 см.
Сторона основания а = 6/cos 30° = 6/(√3/2) = 12/√3 = 4√3 см.
Площадь основания So = a²√3/4 = 48√3/4 = 12√3 см².
Получаем ответ:
Объём пирамиды V = (1/3)SoH = (1/3)*(12√3)*(2√3) = 8*3 = 24 см³.