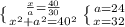
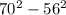= 1764, второй катет равен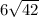 
5 х - длина 1-й диагонали
12 х - длина 2-й диагонали
Площадь ромба 120 см² равна половине произведения диагоналей.
120 = 0,5·5x·12x
120 = 30 х²
х² = 4
х = 2
5 х = 10 см - длина 1-й диагонали
12 х = 24 см - длина 2-й диагонали
Диагонали ромба разбивают его на 4 равных прямоугольных треугольника.
В каждом тр-ке катетами являются половинки диагоналей, равные 5 см и 12 см, а гипотенузой является сторона ромба а.
Тогда по теореме Пифагора:
а² = 25 + 144 = 169
а = 13 см - сторона ромба
Р = 4 а = 4·13 = 52 см - периметр ромба
Дана пирамида с площадью основания So = 18√3.
Если все двугранные углы при рёбрах основания равны α = 30 градусов, то площадь Sбок боковой поверхности пирамиды равна:
Sбок = Sо/cos α = 18√3 /(√3 /2) = 36 кв.ед.