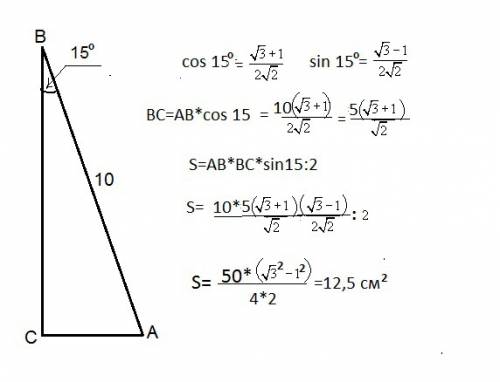
Четырёхугольник ABCD вписан в окружность.
∠В : ∠D = 1 : 5
∠A < в 2 раза ∠С.
Найти:∠А - ? ; ∠В - ? ; ∠С - ? ; ∠D - ? .
Решение:Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.
Около четырёхугольника ABCD описана окружность, по условию ⇒ ∠B + ∠D = 180˚; ∠A + ∠C = 180°.
Найдём ∠B и ∠D:
Пусть х - ∠В, тогда 5х - ∠D. (∠B : ∠D = 1 : 5, по условию)
Как я написала ранее, ∠B + ∠D = 180˚, по свойству.
х + 5х = 180
6х = 180
х = 30
30° - ∠B.
⇒ ∠D = 30˚ * 5 = 150˚.
Найдём ∠А и ∠С:
Пусть х - ∠А, тогда 2х - ∠С.
Как я написала ранее, ∠А + ∠С = 180°, по свойству.
х + 2х = 180
3х = 180
х = 60
60° - ∠А.
⇒ ∠С = 60° * 2 = 120°
ответ: 30°; 150°; 60°; 120°.
Дано:
ABC-равнобедренный треугольник
AB=BC=x+18
AC=x
Найти:AB,BC,AC
54=(x+18)*2+x
54=36+2x+x
54-36=3x
18=3x
x=6
ответ:AC=6,AB=BC=6+18=24