Дан треугольник АВС, угол А = 45 градусов, АВ =8 √2 и АС = 18.
Поместим его в прямоугольную систему координат точкой А в начало, точка В на оси Ох.
х(В) = AB*cos A = 8√2*(√2/2) = 8.
y(B) = AB*sin A = 8√2*(√2/2) = 8.
Получили координаты вершин.
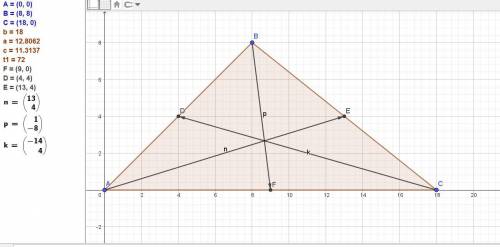
А(0; 0), В(8; 8), С(18; 0).
Находим векторы сторон.
Координаты векторов
АВ ВС АС
х у х у х у
8 8 10 -8 18 0.
По свойству векторов медиана как половина диагонали параллелограмма на векторах сторон равна половине суммы векторов сторон.
Медианы
АА1 ВВ1 СС1
х у х у х у
13 4 1 -8 -14 4.
Модули (длины) медиан равны:
|AA1| = √(13² + 4²) = √(169 + 16) = √185 ≈ 13,60147.
|BB1| = √(1² + (-8)²) = √(1 + 64) = √65 ≈ 8,06226.
|CC1| = √((-14)² + 4²) = √(196 + 16) = √212 ≈ 14,56022.
Круг можно тремя разрезами разделить на 7 частей: Линия каждого разреза пересекается с двумя другими и получится 3•2 части, плюс часть, которая получится между ними (см. рисунок).
Блин также можно разделить на 7 частей, если его не сворачивать. Если первым разрезом поделить блин пополам, затем наложить одну половину на другую и двумя сквозными пересекающимися разрезами разделить эти половини еще на 4 части , то блин можно разделить на 8 частей.
Так как каравай имеет высоту, можно разделить его таким образом:
Первый разрез провести по высоте - получатся две круглые части.
Затем крестообразно провести еще два разреза от края до края и получить наибольшее количество частей, на которое его можно разделить - 8 частей.
Объяснение:
То, что M и N симметричны относительно AB означает, что
1) MN ⊥ AB
2) Если K - точка пересечения MN и AB, то |MK|=|KN|.
Рассмотрим треугольники AKN и AKM.
1. AK - общая сторона
2. |MK| = |KN|
3. Углы AKM и AKN равны (так как оба равны 90°)
Таким образом, треугольники AKN и AKM равны, а значит равны и углы MAK и NAK, то есть луч AB - биссектриса угла MAN