Объяснение:
ЗАДАЧА 1
1 вариант. Нужно построить дугу 120 с транспортира и из любой точки не на этой дуге провести лучи.
2 вариант. Нужно построить дугу 120 ( по т. о вписанном угле) с циркуля или линейки.Например так:
Чтобы разделить окружность радиуса r надо
1)из точки пересечения диаметра с окружностью начертить дополнительную дугу радиуса r.
2) получившиеся точки пересечения соединяем,
3) каждая дуга будет 120 градусов
ЗАДАЧА 2
Пусть одна часть х, тогда меньшая дуга 4х, большая дуга 5х.
Вся окружность 360, 4х+5х=360, х=40.
Меньшая дуга 4*40=160, большая дуга 5*40=200.
Пусть хорда АВ, точка М может лежать на меньшей дуге или на большей.
По т.о вписанном угле получаем:
-Если М лежит на меньшей дуге , то ∠АМВ=1/2*160=80
-Если М лежит на большей дуге , то ∠АМВ=1/2*200=100.
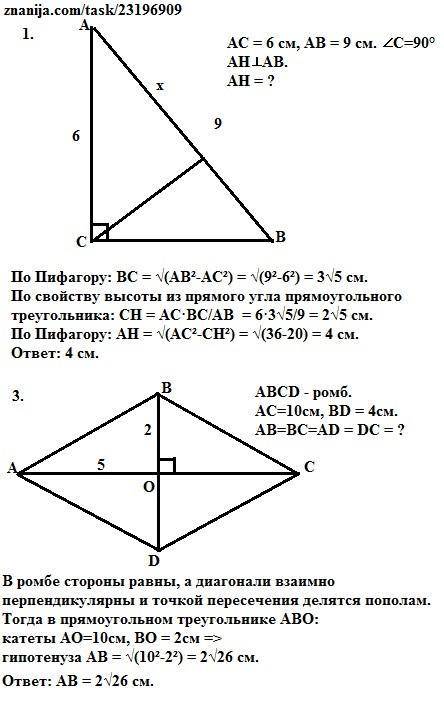
1. 4 см.
2. 84 см.
3. 2√26 см.
Объяснение:
1. По Пифагору: ВС = √(АВ²-АС²) = √(9²-6²) = 3√5 см.
По свойству высоты из прямого угла прямоугольного треугольника:
СН = АС·ВС/АВ = 6·3√5/9 = 2√5 см.
По Пифагору: АН = √(АС²-СН²) = √(36-20) = 4 см.
ответ: 4 см.
2. По Пифагору второй катет равен √(37²-35²) = √(2·72) = 12см. Тогда периметр треугольника (сумма его трех сторон) равен:
37+35+12 = 84см.
ответ: 84см.
3. В ромбе стороны равны, а диагонали взаимно перпендикулярны и точкой пересечения делятся пополам.
Тогда в прямоугольном треугольнике АВО:
катеты АО=10см, ВО = 2см =>
гипотенуза АВ = √(10²-2²) = 2√26 см.
ответ: 2√26 см.
6. Правильные 4-, 5-, 10-, 20-, 25-, 50- угольники.
Объяснение:
Если указывать правильный n-угольник на данных вершинах, то между парами соседних вершин нового многоугольника будет пропущено одинаковое количество k вершин старого многоугольника (выбираем вершины через k). С учетом того, что всего вершин было 100,
n * (k + 1) = 100.
n > 2 (число вершин в новом многоугольнике - n)
100 = 2 * 2 * 5 * 5 = 2² * 3²
Всего разложений на два множителя с учетом порядка:
3 * 3 = 9 (в точности количество различных делителей)
Среди них не подходят те, в которых n=1 или n=2 (они, очевидно, встречаются и ровно по одному разу) и n=100 (исходный 100-угольник). Итого 6 правильных многоугольников.
Можно получить этот же ответ в явном виде.
Распишем всевозможные разложения на два множителя (с учетом порядка) числа 100:
100 = 1 * 100 - n=1, k=99 - не подходит (n > 2)
100 = 2 * 50 - n=2, k=49 - не подходит (n > 2)
100 = 4 * 25 - n=4, k=24 - подходит
100 = 5 * 20 - n=5, k=19 - подходит
100 = 10 * 10 - n=10, k=9 - подходит
100 = 20 * 5 - n=20, k=4 - подходит
100 = 25 * 4 - n=25, k=3 - подходит
100 = 50 * 2 - n=50, k=1 - подходит
100 = 100 * 1 - n=100, k=0 - исходный 100-угольник