Объяснение:
1) На произвольной прямой отложить отрезок, равный длине периметра. Обозначить его АК.
2) От т.А циркулем отметить на АК точку С, АС= длине данного основания.
3). Отрезок СК разделить на две равные части. Для этого из т.С и т.В провести две полуокружности до их пересечения по обе стороны от СК. Точки пересечения соединить прямой ( срединным перпендикуляром). Точку пересечения этой прямой и отрезка СК обозначить М. СМ=МК=длина боковой стороны треугольника.
4). Циркулем с раствором, равным МК, провести из точек А и С дуги до их пересечения. Точку пересечения обозначить В и соединить с т.А и т.С. Треугольник АВС - искомый.
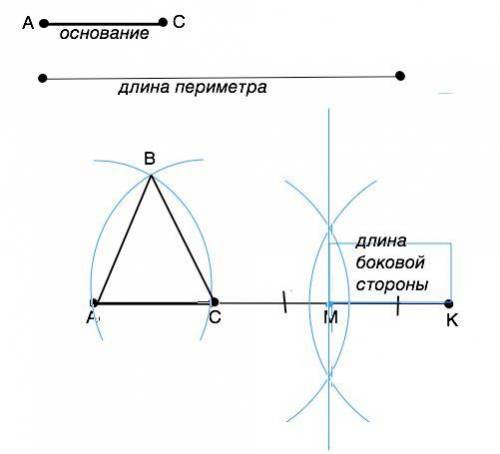
Объяснение:
1) На произвольной прямой отложить отрезок, равный длине периметра. Обозначить его АК.
2) От т.А циркулем отметить на АК точку С, АС= длине данного основания.
3). Отрезок СК разделить на две равные части. Для этого из т.С и т.В провести две полуокружности до их пересечения по обе стороны от СК. Точки пересечения соединить прямой ( срединным перпендикуляром). Точку пересечения этой прямой и отрезка СК обозначить М. СМ=МК=длина боковой стороны треугольника.
4). Циркулем с раствором, равным МК, провести из точек А и С дуги до их пересечения. Точку пересечения обозначить В и соединить с т.А и т.С. Треугольник АВС - искомый.

Глубина пруда в центре 3 2/3 м.
Объяснение:
АВ=ВС=АС=10 м. OK = 1 м. DH=DK (дано).
HC = (√3/2)*10 = 5√3 м.
HO = (1/3)*HC = 5√3/3 м.
НК = √(ОН²+КО²) = 2√21/3 м.
∠ KHO = 90 - ∠ HKO. ∠ D = 180 - 2∠HKO = 2*(90 - ∠ HKO) (так как треугольник HDK равнобедренный) =>
∠ D = 2*∠ KHO. Tg(∠ KHO) = KO/HO =3/5√3 = √3/5.
Tg(2∠ KHO) = 2tg(∠ KHO)/(1 - tg²(∠ KHO)) (по формуле двойного угла) или
TgD= (2√3/5)/(22/25) = 5√3/11. Тогда
TgD=HO/OD => Глубина в центре водоема:
OD = HO/tgD = (5√3/3)/(5√3/11) = 11/3 = 3 2/3 м.