Рассмотрю три решения:
1) Пусть сторона AB = x, тогда AH = 0,5 * x, BH = 2 * (√3) ( по условию )
Тогда по теореме Пифагора: x ² = (0,5 * x) ² + (2 * (√3)) ²
x ² = (1/4 * x ²) + 4 * 3
x ² - (x ² / 4) = 12
(4 * x ² - x ²) / 4 = 12
3 * x ² = 48
x ² = 16
x = 4.
2) Треугольник ABH - прямоугольный, угол BAH = 60°.
sin 60° = BH / AB
AB = BH / sin 60°
AB = (2 * (√3)) / ((√3) / 2)
AB = 4.
3) Медианы в равностороннем треугольнике пересекаются в одной точке и делятся в соотношении 2:1 от вершины. 2/3 часть медианы будет являться радиусом описанной окружности. Значит R = (2 / 3) * 2 * (√3) = (4 * (√3)) / 3.
По теореме синусов:
2R = AB / sin 60°
(2 * 4 * (√3)) / 3 = AB / ((√3) / 2)
AB = (√3) / 2 * (8 * (√3) / 3)
AB = 4.
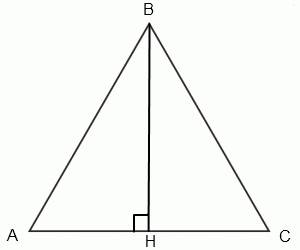
Углы при основании равны по 45°, угол при вершине 90°
Объяснение:
Пусть угол при основании равнобедренного треугольника равен х, тогда внешний угол при основании равнобедренного треугольника равен 3х.
Эти углы смежные, их сумма равна 180°.
х + 3х = 180°
4х = 180°
х = 45° - угол при основании
3х = 3 · 45° = 135° внешний угол при основании
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
Внешний угол при основании равнобедренного треугольника равен 135°, один из не смежных с ним углов при основании равен 45°, тогда угол при вершине равен
135° - 45° = 90°.