MD = 2,5 см
Объяснение:
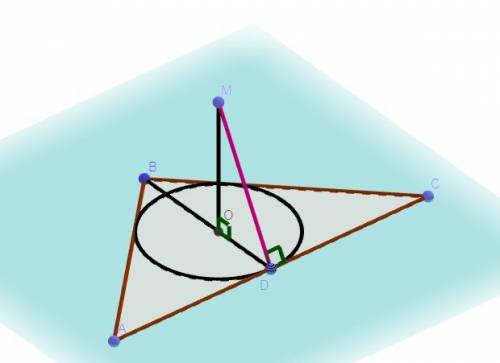
Дано: AC = 6 см, AB = BC = 5 см, О - центр вписаного кола, OM ⊥ ABC,
OM = 2 см, MD ⊥ AC.
Знайти: MD - ?
Розв'язання: За теоремою про три перпендикуляри так як OM ⊥ ABC,
MD ⊥ AC, тоді OD ⊥ AC, отже OD - радіус вписаного кола, так як радіус вписаного кола проведений з центра кола до сторони трикутника і перпендикулярний до сторони. Нехай півпериметр трикутника p, тоді
p = 0,5 * PΔABC = 0,5(AB + BC + AC) = 0,5(5 + 5 + 6) = 0,5 * 16 = 8 см.
За формулами площі триутника слідує наступне:
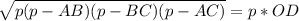
 см.
см.
Розглянемо трикутник ΔMOD. За теоремою Піфагора:
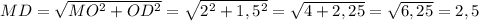 см.
см.
Відповідь: Б) Не можна
Пояснення:
Припустимо, що через точку С можна провести дві різні прямі, кожна з яких перетинає мимобіжні прямі a та b.
Через проведені дві прямі (що перетинаються в точці С) проходить площина. Всі точки перетину двох прямих з прямими a та b також лежать в цій площині, отже, й самі прямі a та b також лежать в одній площині.
Але, з умови прямі a та b - мимобіжні, тому вони не можуть лежати в одній площині. Маємо суперечність.
Отже, початкове припущення є хибним, отже, через точку С не можна провести дві різні прямі, кожна з яких перетинає мимобіжні прямі a та b.
Ад=60° потому что если это равнобедреная тропеция то его 2 стороны равны