Пусть А(-1;10); В(1;10), С (16;2), D(-7;2)
АВ=√((-1-1)²+(10-10)²)=2
ВС =√((16-1)²+(2-10)²)=√(225+64)=17
СD=√((23)²+0²)=23
АD=√((-7+1)²+(2-10)²)=10
Р=АВ+ВС+СD+АD= 2+17+23+10=52
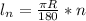, где n - градусная мера соответственного центрального угла.
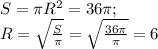, где S - площадь круга.
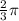см.
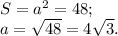
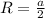, где a - сторона квадрата.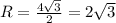
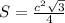, где c - сторона правильного треугольника.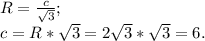
.
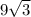см.
В основе прямой призмы лежит равнобедренная трапеция с основаниями 4см и 10 см и боковой стороной 5 см. Боковое ребро призмы равно 10 см. Вычислите полную поверхность призмы.
Объяснение:
В прямой призме боковое ребро перпендикулярно площади основания.
S( полной)=S(боковой)+2S(основания);
S(боковой)=Р(основания)*h, где h-ребро боковое призмы;
S(основания)=S(трапеции)=1/2*(а+в)*h ,где h-высота трапеции
S(боковой)=(4+10+2*5)*10=240 (см²).
АВСД-равнобедренная трапеция АВ=СД=5 см ; пусть ВН⊥АД, СК⊥АД ⇒ АН=(10-4):2=3 (см)
ΔАВН-прямоугольный , по т. Пифагора ВН=√(5²-3²)=4 (см).
S(трапеции)=1/2*(4+10)*4=28(см²)
S( полной)=240+2*28=296(см²)
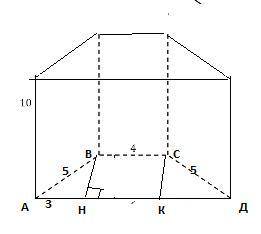
на фото
Объяснение: