Представим отношение в виде: 11х и 7х
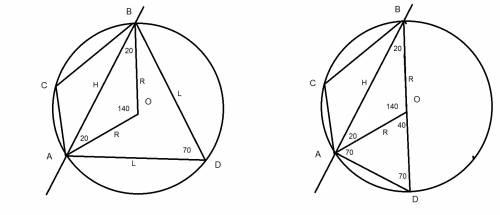
11х+7х=360 градусов (вся окр) Тогда х=20 и меньшая дуга равна 140 гр.
Угол вписанный равен половине дуги и этот угол равен 140:2=70!
ответ: 70 градусов.
достроим прямоугольник до квадрата со стороной a + b, как показано на рисунке 1.
так как площадь квадрата равна квадрату его стороны, то площадь этого квадрата равна (a + b)2.с другой стороны, этот квадрат составлен из данного прямоугольника с площадью s, равного ему прямоугольника с площадью s (так как, по свойству площадей, равные многоугольники имеют равные площади) и двух квадратов с площадями a2 и b2. так как четырехугольник составлен из нескольких четырехугольников, то, по свойству площадей, его площадь равна сумме площадей этих четырехугольников: (a + b)2 = s + s + a2 + b2, или a2 + 2ab + b2 = 2s + a2 + b2.отсюда получаем: s = ab, что и требовалось доказать.
Пусть 1 часть=x,тогда
7x+11x=360°
18x=360°
X=20°
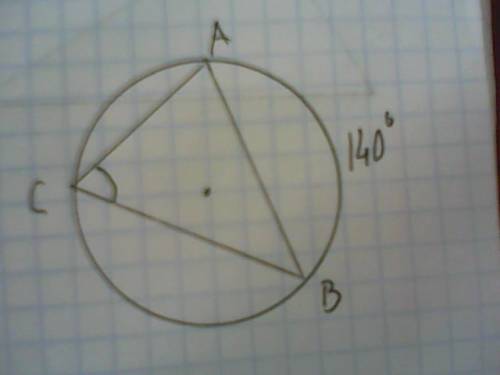
Угловые велечины дуг
7x=7×20=140°
11x=11×20=220°
Угол ACB=1/2дуги AB=1/2×140°=70°