Два игрока, Петя и Ваня, играют в следующую игру.
Перед игроками лежат три кучи камней. Игроки ходят
по очереди, первый ход делает Петя. За один ход
игрок может добавить в одну из куч один камень или
увеличить количество камней в куче в три раза (+1 или *3).
Например, пусть в первой куче 10 камней, во второй
7, а в третьей 4 камня; такую позицию в игре будем
обозначать (10, 7, 4). Тогда за один ход можно
получить любую из шести позиций: (11, 7, 4), (30, 7,
4), (10, 8, 4), (10, 21, 4), (10, 7, 5), (10, 7, 12). Чтобы
делать ходы, у каждого игрока есть неограниченное
количество камней.

Победителем считается игрок, сделавший последний
ход, то есть первым получивший позицию, в которой
в кучах будет 50 или больше камней.
В начальный момент в первой куче было 9 камней, во
второй куче — 10 камней, а в третьей S камней, 1
≤ S ≤ 30.

Будем говорить, что игрок имеет выигрышную
стратегию, если он может выиграть при любых ходах
противника. Описать стратегию игрока — значит,
описать, какой ход он должен сделать в любой
ситуации, которая ему может встретиться при
различной игре противника.

Задание: Укажите такое значение S, при котором у
Вани есть выигрышная стратегия, позволяющая ему
выиграть ВТОРЫМ ходом при любой игре
Пети. Для указанного значения S опишите
выигрышную стратегию Вани.

👇

Открыть все ответы

Ответ:

darya2401

03.01.2020

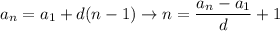
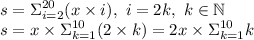
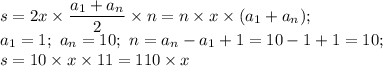
1.В содержательном подходе количество информации, заключённое в сообщении, определяется объёмом знаний, который это сообщение несёт получающему его человеку. Один бит - это минимальная единица измерения количества информации. Сообщение, уменьшающее неопределённость знания в два раза, несёт один бит информации.

2.Вероятностный подход предполагает, что возможные события имеют различные вероятности реализации. ... Качественная связь между вероятностью события и количеством информации в сообщении состоит в следующем: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.

3.Эта единица называется бит. Сообщение, уменьшающее неопределенность знаний в два раза, несет 1 бит информации. Неопределенность знаний о некотором событии – это количество возможных результатов события.

4.Формула Хартли или хартлиевское количество информации или мера Хартли - логарифмическая мера информации, которая определяет количество информации, содержащееся в сообщении. ... Формула была предложена Ральфом Хартли в 1928 году как один из научных подходов к оценке сообщений.

5.Случа́йное собы́тие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.

4,4(67 оценок)

Ответ:

penguin2517

03.01.2020

1.1. Количество нечетных чисел в заданном промежутке можно легко найти, зная что нечетные числа следуют через одно, чередуясь с четными. Конечно, можно написать в программе цикл и перебрать все нечетные элементы, каждый раз добавляя по +1 в счетчик количества, но гораздо проще воспользоваться знаниями из математики. Легко видеть, что нечетные числа образуют арифметическую прогрессию с разностью d=-2, начальный член a1=7, а конечный член an=-3.
Вспомним формулу для n-го члена арифметической прогрессии и получим из нее n.
$\displaystyle a_n=a_1+d(n-1) \to n= \frac{a_n-a_1}{d}+1$
В соответствии с условиями нашей задачи это будет верно, если a1 и an - нечетные. Если a1 четное, то его надо уменьшить на 1. Аналогично, если an четное, его надо увеличить на 1. Таким образом, мы получаем алгоритм, пригодный для быстрого определения количества нечетных чисел на любом интервале с целочисленными границами.
Ниже приводится соответствующая программа.

program p11;
var
a,b,n:integer;
begin
Write('Введите границы интервала: '); Readln(a,b);
{ защита от неверного порядка ввода }
if a<b then begin n:=a; a:=b; b:=n end;
{ если надо, корректируем границы на нечет }
if (a mod 2)=0 then a:=a-1;
if (b mod 2)=0 then b:=b+1;
{ сам расчет }
n:=(a-b) div 2 + 1;
Writeln('Количество нечетных чисел на интервале равно ',n)
end.

Тестовое решение:
Введите границы интервала: -3 7
Количество нечетных чисел на интервале равно 6

1.2 В противоположность предложенному решению, где сначала надо было думать, можно использовать "метод грубой силы" (программисты называют его "брутфорс" - от английского bruteforce), т.е. программировать ни о чем не думая.
Ниже - пример такого решения. Оно более короткое, но при больших интервалах время решения окажется на несколько порядков больше.

program p12;
var
a,b,i,k:integer;
begin
Write('Введите границы интервала: '); Readln(a,b);
{ защита от неверного порядка ввода }
if a<b then begin k:=a; a:=b; b:=k end;
k:=0;
for i:=a downto b do
if (i mod 2)<>0 then k:=k+1;
Writeln('Количество нечетных чисел на интервале равно ',k)
end.

Тестовое решение:
Введите границы интервала: -3 7
Количество нечетных чисел на интервале равно 6

2.1. Тут задача на первый взгляд стандартная и вроде бы думать нечего - в цикле накапливаем сумму:

program p21;
var
i:integer;
x,s:real;
begin
Write('Введите значение x: '); Readln(x);
s:=0; i:=2;
while i<=20 do begin s:=s+i*x; i:=i+2 end;
Writeln('Cумма членов последовательности равна ',s)
end.

Тестовое решение:
Введите значение x: 2.15
Cумма членов последовательности равна 236.5

2.2. Но и тут есть место для размышлений. Опять вспоминаем математику.
$\displaystyle s=\Sigma_{i=2}^{20}(x\times i), \ i=2k, \ k \in 
\mathbb N \\ s=x\times \Sigma_{k=1}^{10}(2\times 
k)=2x\times\Sigma_{k=1}^{10}k$
Но полученная сумма - это сумма арифметической прогрессии с начальным членом, равным единице, конечным членом, равным 10 и разностью 1. Формула такой суммы известна и мы продолжаем преобразования.
$\displaystyle s=2x\times \frac{a_1+a_n}{2}\times n=n\times 
x\times(a_1+a_n); \\ a_1=1; \ a_n=10; \ n=a_n-a_1+1=10-1+1=10; \\ 
s=10\times x\times11=110\times x$
Теперь можно и программу написать.

program p22;
var
x:real;
begin
Write('Введите значение x: '); Readln(x);
Writeln('Cумма членов последовательности равна ',110*x)
end.

Тестовое решение:
Введите значение x: 2.15
Cумма членов последовательности равна 236.5

Пары приведенных решений призваны показать, что первое пришедшее в голову решение обычно всегда не лучшее. А еще - что для качественного программирования надо учить математику.

4,5(76 оценок)

Это интересно:

Хобби-и-рукоделие

16.01.2022

Угловые закладки своими руками: простой и креативный способ сохранить страницу...

Финансы-и-бизнес

18.09.2022

Как вычислить период оборота запасов: практическое руководство...

19.11.2022

Как избавиться от одержимости человеком: советы от психологов и опытных людей...

Образование-и-коммуникации

04.01.2021