В этот раз любитель паркура Василий столкнулся с неожиданным препятствием при попытке попасть домой — старая лестница в его подъезде наполовину обвалилась. Всего в ему нужно подняться на ступенек вверх, но ступеньки с номерами 1,…, разрушены, и на них наступать нельзя. Поскольку Василий — любитель паркура, он хочет сделать подъем интересным и будет прыгать только на или ступенек вверх.

Посчитайте, сможет ли Василий добраться до своей квартиры или ему придется ждать, пока лестницу починят или паркур выйдет из моды. Изначально он находится на нулевой ступеньке, а чтобы попасть в квартиру, ему надо оказаться ровно на -ной.

Входные данные
В первой строке через пробел даны два числа и — общее количество ступенек и количество сломанных ступенек, соответственно (1⩽<⩽106).

Во второй строке перечислены через пробел чисел в порядке возрастания — номера сломанных ступенек (1⩽⩽).

Во третьей строке заданы числа и — количество ступенек, на которое Василий умеет перемещаться вперед (1⩽,⩽106).

Выходные данные
Выведите «YES» (без кавычек), если Василий сможет попасть в свою квартиру, и «NO» иначе.

👇

Увидеть ответ

Ответ:

vadim369

05.05.2023

я думаю он сможет добраться

ну в крайнем случае доползёт)

4,6(64 оценок)

Открыть все ответы

Ответ:

natalijamatijch

05.05.2023

Каждая из компонент связности должна быть кликой (иначе говоря, каждые две вершины в одной компоненте связности должны быть связаны ребром). Если в i-ой компоненте связности n_i

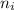вершин, то общее число рёбер будет суммой по всем компонентам связности: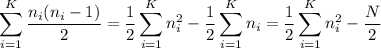

$\displaystyle \sum_{i=1}^K\frac{n_i(n_i-1)}2=\frac12\sum_{i=1}^K n_i^2-\frac12\sum_{i=1}^Kn_i=\frac12\sum_{i=1}^K n_i^2-\frac N2$

Требуется найти максимум этого выражения (т.е. на самом деле - максимум суммы квадратов) при условии, что сумма всех ni равна N и ni - натуральные числа.

Если K = 1, то всё очевидно - ответ N(N - 1)/2. Пусть K > 1.

Предположим, n1 <= n2 <= ... <= nK - набор чисел, для которых достигается максимум, и n1 > 1. Уменьшим число вершин в первой компоненте связности до 1, а оставшиеся вершины "перекинем" в K-ую компоненту связности. Вычислим, как изменится сумма квадратов:
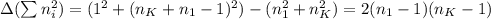
$\Delta(\sum n_i^2)=(1^2+(n_K+n_1-1)^2)-(n_1^2+n_K^2)=2(n_1-1)(n_K-1)$
Поскольку по предположению n1 > 1 (тогда и nK > 1), то сумма квадратов увеличится, что противоречит предположению о том, что на выбранном изначально наборе достигается максимум. Значит, максимум достигается, если наименьшая по размеру компонента связности - изолированная вершина. Выкинем эту компоненту связности, останутся K - 1 компонента связности и N - 1 вершина. Будем продолжать так делать, пока не останется одна вершина, тогда получится, что во всех компонентах связности кроме последней должно быть по одной вершине.

Итак, должно выполняться
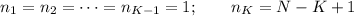
$n_1=n_2=\cdots=n_{K-1}=1;\qquad n_K=N-K+1$

Подставив в исходную формулу, получаем
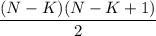
$\displaystyle\frac{(N-K)(N-K+1)}{2}$

Это и есть ответ.

4,7(55 оценок)

Ответ:

Ytbjfdg

05.05.2023

Var
a:array[1..100,1..100] of integer;
c:array[1..20,1..20] of real;
b:array[1..20,1..20] of real;
i,j,n,k:integer;
t:real;
r:integer;
begin
randomize;
t:=0;
Writeln('Введите порядок матрицы: ');
readln(n);
for i:=1 to n do
for j:=1 to n do
begin
a[i, j] := random(10);
end;
for i:=1 to n do
for j:=1 to n do
begin
b[i,j]:=1/i+j-1;
end;
for i:=1 to n do
for j:=1 to n do
begin
for k:=1 to n do
begin
t :=t+a[i,k]*b[k, j];
end;
c[i,j]:=t;
t:=0;
end;
for i:=1 to n do
begin
for j:=1 to n do
begin
write(' ',c[i,j]:2:2);
end;
Writeln;
end;

end.

4,5(82 оценок)

Это интересно:

Стиль-и-уход-за-собой

28.01.2022

Как окрасить волосы в технике Dip-Dye при помощи Kool Aid?...

Философия-и-религия

03.06.2020

Практики тибетского буддизма: как начать и что ожидать...

Компьютеры-и-электроника

27.05.2020

Как увеличить масштаб страницы браузера...

Компьютеры-и-электроника