
Координаты даны в двоичной системе счисления, поэтому переводим их в десятичную.
Потом сортируем по порядку по номерам точек.
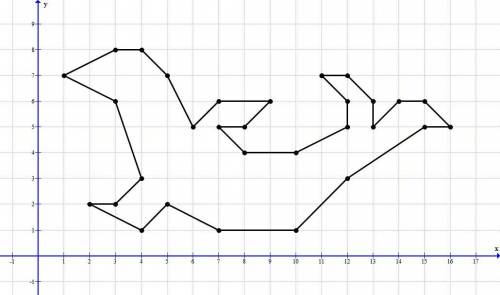
И отмечаем точки на графике, соединяя соседние отрезком.
Я все эти преобразования сделал в таблице Эксель.
Саму таблицу и картинку, полученную после нанесения всех точек смотри внизу.
А вот координаты точек, отсортированные и в десятичной системе:
№ x y
1 11 7
2 12 7
3 13 6
4 13 5
5 14 6
6 15 6
7 16 5
8 15 5
9 12 3
10 10 1
11 7 1
12 5 2
13 4 1
14 2 2
15 3 2
16 4 3
17 3 6
18 1 7
19 3 8
20 4 8
21 5 7
22 6 5
23 7 6
24 9 6
25 8 5
26 7 5
27 8 4
28 10 4
29 12 5
30 12 6
31 11 7
При любых A, B и C данное выражение истинно.
Объяснение:Для начала упростим эквивалентность и импликацию.
Экивалентность (≡) раскрывается вот так:
x ≡ y = x ∧ y ∨ -x ∧ -yПрименим к нашим данным:
A ∧ B ≡ B ∧ C = (A ∧ B ∧ B ∧ C) ∨ ( -(A ∧ B) ∧ -(B ∧ C) ) =
Первая скобка упрощается по закону повторения (B ∧ B = B), а вторая скобка, а точнее отрицание раскрывается по закону де Моргана:
= (A ∧ B ∧ C) ∨ ( -A ∨ -B ∧ -B ∨ -C) =
По закону исключения третьего (A ∨ -A = 1) упрощаем запись:
= 1
На самом деле я здесь очень сильно упростил запись. На самом деле нам не помешало бы раскрыть данную дизъюнкцию, "перемножив" A на -A, A на -B, A на -C, B на -A и так далее. Но в итоге данная запись сократится в единицу.
Теперь рассмотрим импликацию (⇒):
(x ⇒ y) = -x ∧ yПрименим к нашим данным:
(-C ⇒ A) = -(-C) ∧ A =
По закону двойного отрицания (-(-C) = C):
C ∧ A
Итого наш пример принял такой вид:
1 ∨ C ∧ A
Данное выражение всегда истинно, поскольку дизъюнкция истинна в том случае, когда одно из выражений истинно, а в нашем случае левая часть (единица), то есть дизъюнкция вседа истинна.
#include <iostream>
using namespace std;
int main() {
setlocale(LC_ALL, "Rus");
double E, x;
cout << "Введите значение переменной x: ";
cin >> x;
E = exp(4 * x / 5) + 2 * sin(7 * log(x + 5 / 3)) - 6 / 11;
cout << E;
return 0;
}