380 / 2 = 190 целых и 0 в остатке
190 / 2 = 95 целых и 0 в остатке
95 / 2 = 47 целых и 1 в остатке
47 / 2 = 23 целых и 1 в остатке
23 / 2 = 11 целых и 1 в остатке
11 / 2 = 5 целых и 1 в остатке
5 / 2 = 2 целых и 1 в остатке
2 / 2 = 1 целых и 0 в остатке
1 / 2 = 0 целых и 1 в остатке
380₁₀ = 101111100₂
237 / 2 = 118 целых и 1 в остатке
118 / 2 = 59 целых и 0 в остатке
59 / 2 = 29 целых и 1 в остатке
29 / 2 = 14 целых и 1 в остатке
14 / 2 = 7 целых и 0 в остатке
7 / 2 = 3 целых и 1 в остатке
3 / 2 = 1 целых и 1 в остатке
1 / 2 = 0 целых и 1 в остатке
237₁₀ = 11101101₂
101111100₂ - 11101101₂ = 10001111₂
10001111₂ = 1*2⁰ + 1*2¹ + 1*2²+ 1*2³ + 0*2⁴ + 0*2⁵ + 0*2⁶ + 1*2⁷ =
1 + 2 + 4 + 8 + 0 + 0 + 0 + 128 = 1 + 2 + 4 + 8 + 128 = 143
380₁₀ - 237₁₀ = 143₁₀
Объяснение:
Цветные цифры действия в уме. Точка занимание из старшего разряда.
Таблица двоичного вычитания
0₂ – 0₂ = 0₂
1₂ – 0₂ = 1₂
1₂ – 1₂ = 0₂
10₂ – 1₂ = 1₂

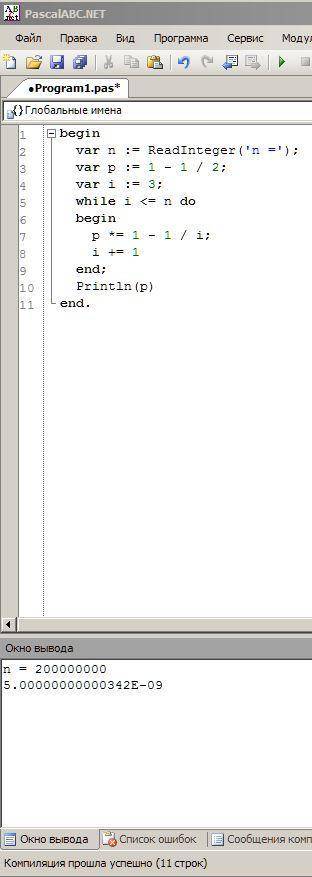
===== PascalABC.NET =====
begin
var n := ReadInteger('n =');
var p := 1 - 1 / 2;
var i := 3;
while i <= n do
begin
p *= 1 - 1 / i;
i += 1
end;
Println(p)
end.
Объяснение:
Хороший "страдать фигней", программируя подобные задачи.
Ведь понятно, что (1 - 1/2) (1 - 1/3) ( 1 - 1/4) ... (1 - 1/n) всегда равно 1/n
В самом деле? 1/2 × 2/3 × 3/4 × 4/5 × ... (n-1)/n = 1/n, потому что соседние члены взпимно сокращаются.
Правда, задав достаточно большое n, можно убедиться, что арифметика вещественных чисел небезупречна в точности. В приведенном примере для n = 2 миллиарда получаем погрешность уже в 13-й цифре.
var
a:array [1..20] of real;
i,b,count:integer;
p:real;
begin
a[1]:=0.3; a[11]:=36;
a[2]:=5; a[12]:=13;
a[3]:=68; a[13]:=15;
a[4]:=-3; a[14]:=28;
a[5]:=32; a[15]:=-0.7;
a[6]:=-80; a[16]:=-36;
a[7]:=-9; a[17]:=-0.3;
a[8]:=-26; a[18]:=8;
a[9]:=-9; a[19]:=15;
a[10]:=40; a[20]:=-7;
b:=5; count:=0; p:=1;
for i:=1 to 20 do
begin
write(a[i],' ');
if ) then
begin
inc(count);
p:=p*a[i];
end;
end;
writeln;
writeln('count: ',count,' Pr: ',p);
end.